题目内容
已知数列{an}的各项都为正数,Sn=
+
+…+
.
(1)若数列{an}是首项为1,公差为
的等差数列,求S67;
(2)若Sn=
,求证:数列{an}是等差数列.
| 1 | ||||
|
| 1 | ||||
|
| 1 | ||||
|
(1)若数列{an}是首项为1,公差为
| 3 |
| 2 |
(2)若Sn=
| n | ||||
|
考点:数列的求和,等差关系的确定,等差数列的性质
专题:等差数列与等比数列
分析:(1)运用等差数列的通项公式,求出an,考虑
=
(
-
),再化简Sn,再求S67;
(2)运用数学归纳法证明,当n=2时,化简得到a2-a3=a1-a2即a1,a2,a3成等差数列,令n=k时,且ak+1=a1+kd,证明当n=k+1时,即k(ak+2-ak+1)=ak+1-a1,由假设即得ak+2-ak+1=d,从而得证.
| 1 | ||||
|
| 2 |
| 3 |
| an+1 |
| an |
(2)运用数学归纳法证明,当n=2时,化简得到a2-a3=a1-a2即a1,a2,a3成等差数列,令n=k时,且ak+1=a1+kd,证明当n=k+1时,即k(ak+2-ak+1)=ak+1-a1,由假设即得ak+2-ak+1=d,从而得证.
解答:
(1)解:若数列{an}是首项为1,公差为
的等差数列,
则an=1+
(n-1)=
n-
,
则
=
=
(
-
),
则S67=
(-
+
-
+
+…+
-
)=
(
-
)
=
(
-1).
(2)证明:当n=2时,S2=
=
+
即
=
∴a2-a3=a1-a2即a1,a2,a3成等差数列
令n=k时,
+
+…+
=
且又{ak}为等差数列且ak+1=a1+kd
当n=k+1时,
+
+…
+
=
即有
+
=
k•
=
即k(ak+2-ak+1)=ak+1-a1
∵ak+1=a1+kd即ak+2-ak+1=d
∴n=k+1时,{ak+1}也是等差数列,
综上得,{an}是等差数列.
| 3 |
| 2 |
则an=1+
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
则
| 1 | ||||
|
| ||||
| an+1-an |
| 2 |
| 3 |
| an+1 |
| an |
则S67=
| 2 |
| 3 |
| a1 |
| a2 |
| a2 |
| a3 |
| a68 |
| a67 |
| 2 |
| 3 |
| a68 |
| a1 |
=
| 2 |
| 3 |
| ||
| 2 |
(2)证明:当n=2时,S2=
| 2 | ||||
|
| 1 | ||||
|
| 1 | ||||
|
即
| ||||||||
(
|
| ||||||||
(
|
∴a2-a3=a1-a2即a1,a2,a3成等差数列
令n=k时,
| 1 | ||||
|
| 1 | ||||
|
| 1 | ||||
|
| k | ||||
|
当n=k+1时,
| 1 | ||||
|
| 1 | ||||
|
| 1 | ||||
|
| 1 | ||||
|
| k+1 | ||||
|
即有
| k | ||||
|
| 1 | ||||
|
| k+1 | ||||
|
k•
| ||||||||
(
|
| ||||||||
(
|
即k(ak+2-ak+1)=ak+1-a1
∵ak+1=a1+kd即ak+2-ak+1=d
∴n=k+1时,{ak+1}也是等差数列,
综上得,{an}是等差数列.
点评:本题主要考查等差数列的通项和裂项相消求和法,同时考查运用数学归纳法证明数列问题,注意解题步骤,注意运用假设,本题属于中档题.

练习册系列答案
相关题目
下列命题中,真命题是( )
A、存在x0∈R,sin2
| ||||||
| B、任意x∈(0,π),sinx>cosx | ||||||
| C、任意x∈(0,+∞),x2+1>x | ||||||
| D、存在x0∈R,x02+x0=-1 |
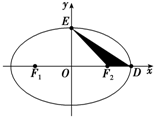 如图F1、F2为椭圆C:
如图F1、F2为椭圆C: