题目内容
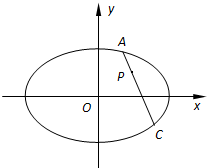 如图所示,在平面直角坐标系xOy中,过椭圆E:
如图所示,在平面直角坐标系xOy中,过椭圆E:| x2 |
| 4 |
| y2 |
| 3 |
| AP |
| PC |
(1)求椭圆E的离心率;
(2)当点C恰为椭圆的右顶点时,试确定对应λ的值;
(3)当λ=1时,求直线AC的斜率.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)因为a2=4,b2=3,由此能求出离心率.
(2)因为C(2,0),所以直线PC的方程为y=-x+2,由
,能求出λ=
.
(3)
=
,设A(x1,y1),C(x2,y2),利用点差法能求出kAC=-
.
(2)因为C(2,0),所以直线PC的方程为y=-x+2,由
|
| 5 |
| 7 |
(3)
| AP |
| PC |
| 3 |
| 4 |
解答:
(本小题满分16分)
解:(1)因为a2=4,b2=3,
所以c2=1,即a=2,c=1,
所以离心率e=
=
.(4分)
(2)因为C(2,0),所以直线PC的方程为y=-x+2,…(6分)
由
,解得A(
,
),…(8分)
代入
=λ
中,得λ=
.…(10分)
(3)因为λ=1,所以
=
,
设A(x1,y1),C(x2,y2),
则x1+x2=2,y1+y2=2,…(12分)
又
+
=1,
+
=1,
两式相减,得
+
=0,
即
+
=0,
从而
=-
,即kAC=-
.…(16分)
解:(1)因为a2=4,b2=3,
所以c2=1,即a=2,c=1,
所以离心率e=
| c |
| a |
| 1 |
| 2 |
(2)因为C(2,0),所以直线PC的方程为y=-x+2,…(6分)
由
|
| 2 |
| 7 |
| 12 |
| 7 |
代入
| AP |
| PC |
| 5 |
| 7 |
(3)因为λ=1,所以
| AP |
| PC |
设A(x1,y1),C(x2,y2),
则x1+x2=2,y1+y2=2,…(12分)
又
| x12 |
| 4 |
| y12 |
| 3 |
| x22 |
| 4 |
| y22 |
| 3 |
两式相减,得
| (x1+x2)(x1-x2) |
| 4 |
| (y1+y2)(y1-y2) |
| 3 |
即
| x1-x2 |
| 4 |
| y1-y2 |
| 3 |
从而
| y1-y2 |
| x1-x2 |
| 3 |
| 4 |
| 3 |
| 4 |
点评:本题考查椭圆的离心率的求法,考查实数的求法,考查直线的斜率的求法,解题时要认真审题,注意点差法的合理运用.

练习册系列答案
相关题目
 在△ABC中,AB=AC,∠CAB=90°,且
在△ABC中,AB=AC,∠CAB=90°,且 如图F1、F2为椭圆C:
如图F1、F2为椭圆C: