题目内容
已知cosα=
,cos(α-β)=-
,0<α<
<β<π.
求:(1)tan2α;(2)β
| 13 |
| 14 |
| 1 |
| 7 |
| π |
| 2 |
求:(1)tan2α;(2)β
考点:两角和与差的余弦函数,二倍角的正切
专题:三角函数的求值
分析:(1)由同角三角函数的基本关系可得tanα,代入二倍角的正切公式计算可得;(2)由角的范围和已知可得sin(α-β),而cosβ=cos[α-(α-β)],代值计算可得其值,由反三角函数可得β.
解答:
解:(1)∵0<α<
,cosα=
,
∴sinα=
=
∴tanα=
=
,
∴tan2α=
=
(2)∵0<α<
<β<π,
∴-π<α-β<0,
∵cos(α-β)=-
<0,
∴∴-π<α-β<-
,
∴sin(α-β)=-
=
,
∴cosβ=cos[α-(α-β)]
=cosαcos(α-β)+sinαsin(α-β)
=
×(-
)+
×
=
∴β=arccos
| π |
| 2 |
| 13 |
| 14 |
∴sinα=
1-(
|
3
| ||
| 14 |
∴tanα=
| sinα |
| cosα |
3
| ||
| 13 |
∴tan2α=
| 2tanα |
| 1-tan2α |
39
| ||
| 71 |
(2)∵0<α<
| π |
| 2 |
∴-π<α-β<0,
∵cos(α-β)=-
| 1 |
| 7 |
∴∴-π<α-β<-
| π |
| 2 |
∴sin(α-β)=-
1-(-
|
4
| ||
| 7 |
∴cosβ=cos[α-(α-β)]
=cosαcos(α-β)+sinαsin(α-β)
=
| 13 |
| 14 |
| 1 |
| 7 |
3
| ||
| 14 |
4
| ||
| 7 |
| 23 |
| 98 |
∴β=arccos
| 23 |
| 98 |
点评:本题考查两角和与差的三角函数公式,涉及二倍角的正切公式,属中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
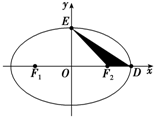 如图F1、F2为椭圆C:
如图F1、F2为椭圆C: