题目内容
14.为丰富少儿文体活动,某学校从篮球,足球,排球,橄榄球中任选2种球给甲班学生使用,剩余的2种球给乙班学生使用,则篮球和足球不在同一班的概率是( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{6}$ |
分析 先求出基本事件总数n=${C}_{4}^{2}$=6,由此求出篮球和足球在同一班的概率,再利用对立事件概率计算公式能求出篮球和足球不在同一班的概率.
解答 解:为丰富少儿文体活动,某学校从篮球,足球,排球,橄榄球中任选2种球给甲班学生使用,
剩余的2种球给乙班学生使用,
基本事件总数n=${C}_{4}^{2}$=6,
篮球和足球在同一班的概率p1=$\frac{{A}_{2}^{2}}{{C}_{4}^{2}}$=$\frac{1}{3}$,
∴篮球和足球不在同一班的概率是:
p=1-p1=1-$\frac{1}{3}$=$\frac{2}{3}$.
故选:C.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意对立事件概率计算公式的合理运用.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
5.某几何体的三视图如图所示,则该几何体的体积为( )


| A. | $\frac{64}{3}$ | B. | 32 | C. | 64 | D. | $\frac{32}{3}$ |
9.将函数y=$\sqrt{3}$cosx+sinx(x∈R)的图象向左平移m(m>0)个单位长度后,所得到的图象关于y轴对称,则m的最小值是( )
| A. | $\frac{π}{3}$ | B. | $\frac{π}{12}$ | C. | $\frac{π}{6}$ | D. | $\frac{5π}{6}$ |
7.已知p:?x∈[1,2],x2-a≥0,q:方程x2+2ax+2-a=0有实数解,若p且q为真命题,则实数a的取值范围是( )
| A. | a≤-2或a=1 | B. | a≤2或1≤a≤2 | C. | a≥1 | D. | -2≤a≤1 |

 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,且AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,且N为PC的中点.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,且AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,且N为PC的中点.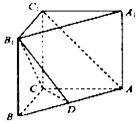 如图,直三棱柱ABC-A1B1C1中,AC=4,BC=3,AA1=4,AC⊥BC,点D在线段AB上.
如图,直三棱柱ABC-A1B1C1中,AC=4,BC=3,AA1=4,AC⊥BC,点D在线段AB上.