题目内容
对于正项数列{an},若
≥q对一切n∈N*恒成立,则an≥a1•qn-1对n∈N*也恒成立是真命题.
(1)若a1=1,an>0,且
≥3c(c≠
,c≠1),求证:数列{an}前n项和Sn≥
;
(2)若x1=4,xn=
(n≥2,n∈N*),求证:3-(
)n-1≤xn≤3+(
)n-1.
| an+1 |
| an |
(1)若a1=1,an>0,且
| an+1 |
| an |
| 1 |
| 3 |
| 1-(3c)n |
| 1-3c |
(2)若x1=4,xn=
| 2xn-1+3 |
| 2 |
| 3 |
| 2 |
| 3 |
考点:数列的求和
专题:等差数列与等比数列,不等式
分析:(1)首先对关系式进行恒等变换,进一步利用等比数列的前n项和公式求解.
(2)先对不等式进行恒等变换,然后求出结果.
(2)先对不等式进行恒等变换,然后求出结果.
解答:
证明:(1)∵
≥3c,
∴an≥a1•(3c)n-1,
∴a2≥3c,a3≥9c2,…an≥(3c)n-1,
Sn=a1+a2+…+an≥1+3c+9c2+(3c)n-1,
∴Sn≥
;
(2)|xn-3|=|
-3|=|
|=
,
∴|xn-3|≤
|xn-1-3|,
∴|xn-3|≤|x1-3|•(
)n-1,
∴|xn-3|≤(
)n-1
∴3-(
)n-1≤xn≤3+(
)n-1.
| an+1 |
| an |
∴an≥a1•(3c)n-1,
∴a2≥3c,a3≥9c2,…an≥(3c)n-1,
Sn=a1+a2+…+an≥1+3c+9c2+(3c)n-1,
∴Sn≥
| 1-(3c)n |
| 1-3c |
(2)|xn-3|=|
| 2xn-1+3 |
(
| ||||
|
| 2|xn-1-3| | ||
|
∴|xn-3|≤
| 2 |
| 3 |
∴|xn-3|≤|x1-3|•(
| 2 |
| 3 |
∴|xn-3|≤(
| 2 |
| 3 |
∴3-(
| 2 |
| 3 |
| 2 |
| 3 |
点评:本题考查的知识要点:数列前n项和公式的应用,不等式的恒等变换问题,属于中等题型.

练习册系列答案
相关题目
在二项式(2x+1)6的展开式中,系数最大项的系数是( )
| A、20 | B、160 |
| C、240 | D、192 |
已知平面α∥平面β,直线m?平面α,那么直线m与平面β 的关系是( )
| A、直线m在平面β内 |
| B、直线m与平面β相交但不垂直 |
| C、直线m与平面β垂直 |
| D、直线m与平面β平行 |
下列说法正确的是( )
| A、“f(O)=O”是“函数f(x)是奇函数”的充要条件 | ||||||||
| B、“向量a,b,c,若a•b=a•c,则b=c”是真命题 | ||||||||
C、函数f(x)=
| ||||||||
D、“若α=
|
下列命题中的真命题是( )
A、?x∈R,sinx+
| ||
B、?x∈R,
| ||
| C、命题p:“?x∈R,x2-x-1>0”的否定¬p:“?x∈R,x2-x-1≤0” | ||
| D、“ea>eb”是“log2a>log2b”的充要条件 |
某三棱锥的三视图如图所示,且三个三角形均为直角三角形,则xy的最大值为( )
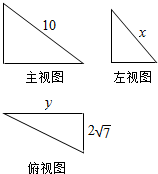

| A、32 | ||
B、32
| ||
| C、64 | ||
D、64
|