题目内容
下列说法正确的是( )
| A、“f(O)=O”是“函数f(x)是奇函数”的充要条件 | ||||||||
| B、“向量a,b,c,若a•b=a•c,则b=c”是真命题 | ||||||||
C、函数f(x)=
| ||||||||
D、“若α=
|
考点:命题的真假判断与应用
专题:简易逻辑
分析:A.例如f(x)=
是奇函数,f(x)=x2是偶函数,即可判断出;
B.若
•
=
•
,则
•(
-
)=0,可得
⊥(
-
),不一定
=
”;
C.f(
)=
+1>0,f(1)=
>0,f(e)=
-1<0,可得在区间(1,e)有零点,即可判断出;
D.利用否命题的定义即可判断出.
| 1 |
| x |
B.若
| a |
| b |
| a |
| c |
| a |
| b |
| c |
| a |
| b |
| c |
| b |
| c |
C.f(
| 1 |
| e |
| 1 |
| 3e |
| 1 |
| 3 |
| e |
| 3 |
D.利用否命题的定义即可判断出.
解答:
解:A.“f(O)=O”是“函数f(x)是奇函数”的既不充分也不必要条件,例如f(x)=
是奇函数,f(x)=x2是偶函数,因此不正确;
B.“向量
,
,
,若
•
=
•
,则
•(
-
)=0,可得
⊥(
-
),不一定
=
”,是假命题,不正确;
C.f(
)=
+1>0,f(1)=
>0,f(e)=
-1<0,可得在区间(1,e)有零点,因此不正确;
D.“若α=
,则sinα=
”的否命题是“若α≠
,则sinα≠
”,正确.
故选:D.
| 1 |
| x |
B.“向量
| a |
| b |
| c |
| a |
| b |
| a |
| c |
| a |
| b |
| c |
| a |
| b |
| c |
| b |
| c |
C.f(
| 1 |
| e |
| 1 |
| 3e |
| 1 |
| 3 |
| e |
| 3 |
D.“若α=
| π |
| 6 |
| 1 |
| 2 |
| π |
| 6 |
| 1 |
| 2 |
故选:D.
点评:本题考查了函数的性质、零点的判定、向量的数量积运算、简易逻辑的判定,考查了推理能力,属于中档题.

练习册系列答案
相关题目
设函数f(x)=ex+2x-4,g(x)=lnx+2x2-5,若实数a,b分别是f(x),g(x)的零点,则( )
| A、g(a)<0<f(b) |
| B、f(b)<0<g(a) |
| C、0<g(a)<f(b) |
| D、f(b)<g(a)<0 |
已知命题P:?x>0,x3>0,那么?P是( )
| A、?x≤0,x3≤0 |
| B、?x>0,x3≤0 |
| C、?x>0,x3≤0 |
| D、?x<0,x3≤0 |
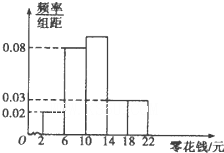 一所中学共有4000名学生,为了引导学生树立正确的消费观,需抽样调查学生每天使用零花钱的数量(取整数元)情况,分层抽取容量为300的样本,作出频率分布直方图如图所示,请估计在全校所有学生中,一天使用零花钱在6元~14元的学生大约有
一所中学共有4000名学生,为了引导学生树立正确的消费观,需抽样调查学生每天使用零花钱的数量(取整数元)情况,分层抽取容量为300的样本,作出频率分布直方图如图所示,请估计在全校所有学生中,一天使用零花钱在6元~14元的学生大约有