题目内容
14.已知O为椭圆中心,F1为椭圆的左焦点,A,B分别为椭圆的右顶点与上顶点,P为椭圆上一点,若PF1⊥F1A,PO∥AB,则该椭圆的离心率为$\frac{\sqrt{2}}{2}$.分析 画出图形,利用已知条件列出方程,求解即可.
解答 解:O为椭圆中心,F1为椭圆的左焦点,A,B分别为椭圆的右顶点与上顶点,P为椭圆上一点,若PF1⊥F1A,PO∥AB,如图:可得:$\frac{P{F}_{1}}{OB}=\frac{O{F}_{1}}{OA}$,$\frac{c}{a}$=$\frac{\frac{{b}^{2}}{a}}{b}$=$\frac{b}{a}$,可得b=c,a=$\sqrt{2}$c,
所以椭圆的离心率为:$\frac{\sqrt{2}}{2}$.
故答案为:$\frac{{\sqrt{2}}}{2}$.
点评 本题考查椭圆的简单性质的应用,考查计算能力.

练习册系列答案
相关题目
4.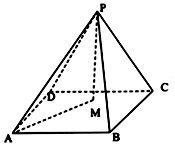 四棱锥P-ABCD中,△PCD为正三角形,底面边长为1的正方形,平面PCD⊥平面ABCD,M为底面内一动点,当$MA=\sqrt{2}PM$时,点M在底面正方形内(包括边界)的轨迹为( )
四棱锥P-ABCD中,△PCD为正三角形,底面边长为1的正方形,平面PCD⊥平面ABCD,M为底面内一动点,当$MA=\sqrt{2}PM$时,点M在底面正方形内(包括边界)的轨迹为( )
 四棱锥P-ABCD中,△PCD为正三角形,底面边长为1的正方形,平面PCD⊥平面ABCD,M为底面内一动点,当$MA=\sqrt{2}PM$时,点M在底面正方形内(包括边界)的轨迹为( )
四棱锥P-ABCD中,△PCD为正三角形,底面边长为1的正方形,平面PCD⊥平面ABCD,M为底面内一动点,当$MA=\sqrt{2}PM$时,点M在底面正方形内(包括边界)的轨迹为( )| A. | 一个点 | B. | 线段 | C. | 圆 | D. | 圆弧 |
2.定义在R上的函数f(x)满足f'(x)-f(x)=x•ex,且$f(0)=\frac{1}{2}$,则$\frac{{x•{e^x}}}{f(x)}$的最大值为( )
| A. | 1 | B. | -$\frac{1}{2}$ | C. | -1 | D. | 0 |
6.函数y=$\frac{sinx}{|sinx|}$+$\frac{|cosx|}{cosx}$+$\frac{tanx}{|tanx|}$的值域是( )
| A. | {1} | B. | {1,3} | C. | {-1} | D. | {-1,3} |
 某飞机失联,经卫星侦查,其最后出现在小岛O附近.现派出四艘搜救船A,B,C,D,为方便联络,船A,B始终在以小岛O为圆心,100海里为半径的圆上,船A,B,C,D构成正方形编队展开搜索,小岛O在正方形编队外(如图).设小岛O到AB的距离为x,∠AOB=α,D船到小岛O的距离为d.
某飞机失联,经卫星侦查,其最后出现在小岛O附近.现派出四艘搜救船A,B,C,D,为方便联络,船A,B始终在以小岛O为圆心,100海里为半径的圆上,船A,B,C,D构成正方形编队展开搜索,小岛O在正方形编队外(如图).设小岛O到AB的距离为x,∠AOB=α,D船到小岛O的距离为d.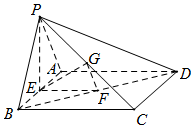 如图,在四棱锥P-ABCD中,底面ABCD是矩形,E,F,G分别是AB,BD,PC的中点,PE⊥底面ABCD.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,E,F,G分别是AB,BD,PC的中点,PE⊥底面ABCD. 如图,在四棱锥S-ABCD中,底面ABCD是棱长为2的正方形,侧棱$SD=2,SA=2\sqrt{2}$,∠SDC=120°.
如图,在四棱锥S-ABCD中,底面ABCD是棱长为2的正方形,侧棱$SD=2,SA=2\sqrt{2}$,∠SDC=120°.