题目内容
已知函数f(x)=ax2+bx+c满足:f(0)=0,对任意x∈R,都有f(x)≥x且f(x)的对称轴为x=-0.5,令g(x)=f(x)-|tx-1|(t>0).
(1)求函数f(x)的表达式;
(2)当t=1时,求函数g(x)的最小值;
(3)求函数g(x)的单调区间.
(1)求函数f(x)的表达式;
(2)当t=1时,求函数g(x)的最小值;
(3)求函数g(x)的单调区间.
考点:二次函数的性质,函数的最值及其几何意义
专题:函数的性质及应用
分析:(1)由f(0)=0,求出c,再由对任意x∈R,都有f(x)≥x恒成立,求出b,利用f(x)的对称轴为x=-0.5,求出a,由此能求出f(x).
(2)由题设知g(x)=
,分x≥1和x<1两种情况进行讨论,能求出g(x)的最小值.
(3)g(x)=
,分x≥
和x<
两种情况进行分析讨论,能求出函数g(x)的单调区间.
(2)由题设知g(x)=
|
(3)g(x)=
|
| 1 |
| t |
| 1 |
| t |
解答:
解:(1)由f(0)=0,得c=0,
且对任意x∈R,都有f(x)≥x恒成立,
即ax2+(b-1)x≥0恒成立,…(2分)
可得b=1,又f(x)的对称轴为x=-0.5,
即-
=-
,得a=1,
所以f(x)=x2+x.…(4分)
(2)g(x)=x2+x-|x-1|=
,…(5分)
当x≥1时,g(x)的最小值为g(1)=2;
当x<1时,g(x)的最小值为g(-1)=-2,
∴g(x)的最小值为-2.…(8分)
(3)g(x)=f(x)-|tx-1|=
,…(9分)
①当x≥
时,g(x)的对称轴为x=
,
≤
,
即0<t≤2时,g(x)在[
,+∞)上单调增,
>
,即t>2时,g(x)在(
,+∞)上单调增,
在(
,
)上单调减.…(11分)
②当x<
时,g(x)的对称轴为x=-
,
因为t>0,则-
<
,
所以g(x)在(-
,
)上单调递增,
在(-∞,-
)上单调递减.…(13分)
综上所述:0<t≤2时,g(x)在(-
,+∞)单调递增,在(-∞,-
)单调减;
t>2时,g(x)在(-
,
),(
,+∞)单调递增,
在(-∞,-
),(
,
)单调递减.…(14分)
且对任意x∈R,都有f(x)≥x恒成立,
即ax2+(b-1)x≥0恒成立,…(2分)
可得b=1,又f(x)的对称轴为x=-0.5,
即-
| b |
| 2a |
| 1 |
| 2 |
所以f(x)=x2+x.…(4分)
(2)g(x)=x2+x-|x-1|=
|
当x≥1时,g(x)的最小值为g(1)=2;
当x<1时,g(x)的最小值为g(-1)=-2,
∴g(x)的最小值为-2.…(8分)
(3)g(x)=f(x)-|tx-1|=
|
①当x≥
| 1 |
| t |
| t-1 |
| 2 |
| t-1 |
| 2 |
| 1 |
| t |
即0<t≤2时,g(x)在[
| 1 |
| t |
| t-1 |
| 2 |
| 1 |
| t |
| t-1 |
| 2 |
在(
| 1 |
| t |
| t-1 |
| 2 |
②当x<
| 1 |
| t |
| t+1 |
| 2 |
因为t>0,则-
| t+1 |
| 2 |
| 1 |
| t |
所以g(x)在(-
| t+1 |
| 2 |
| 1 |
| t |
在(-∞,-
| t+1 |
| 2 |
综上所述:0<t≤2时,g(x)在(-
| t+1 |
| 2 |
| t+1 |
| 2 |
t>2时,g(x)在(-
| t+1 |
| 2 |
| 1 |
| t |
| t-1 |
| 2 |
在(-∞,-
| t+1 |
| 2 |
| 1 |
| t |
| t-1 |
| 2 |
点评:本题考查函数的表达式的求法,考查函数的最小值的求法,考查函数单调区间的求法,解题时要注意分类讨论思想和等价转化思想的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
圆(x-1)2+(y+1)2=2的周长是( )
A、
| ||
| B、2π | ||
C、2
| ||
| D、4π |
在圆x2+y2=4上任取一点P,过点P作x轴的垂线段PD,D为垂足.当点P在圆上运动时,线段PD的中点M的轨迹是( )
| A、椭圆 | B、双曲线 | C、抛物线 | D、圆 |
 某校100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100]
某校100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100]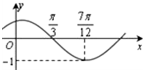 函数f(x)=Asin(ωx+φ)的图象如图所示,为了得到g(x)=-Acosωx的图象,可以将f(x)的图象向右平移
函数f(x)=Asin(ωx+φ)的图象如图所示,为了得到g(x)=-Acosωx的图象,可以将f(x)的图象向右平移