题目内容
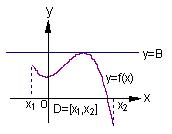
如右图(1)所示,定义在区间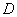 上的函数
上的函数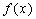 ,如果满
,如果满
足:对 ,
,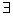 常数A,都有
常数A,都有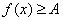 成立,则称函数
成立,则称函数
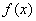 在区间
在区间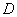 上有下界,其中
上有下界,其中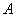 称为函数的下界. (提示:图(1)、
称为函数的下界. (提示:图(1)、
(2)中的常数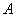 、
、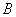 可以是正数,也可以是负数或零)
可以是正数,也可以是负数或零)
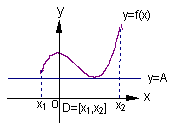 (
(
Ⅰ)试判断函数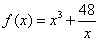 在
在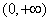 上是否有下界?并说明理由;
上是否有下界?并说明理由;
(Ⅱ)又如具有右图(2)特征的函数称为在区间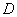 上有上界.
上有上界.
请你类比函数有下界的定义,给出函数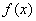 在区间
在区间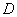 上
上
有上界的定义,并判断(Ⅰ)中的函数在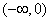 上是否
上是否
有上界?并说明理由;
(Ⅲ)若函数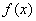 在区间
在区间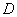 上既有上界又有下界,则称函数
上既有上界又有下界,则称函数
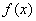 在区间
在区间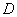 上有界,函数
上有界,函数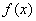 叫做有界函数.试探究函数
叫做有界函数.试探究函数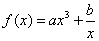 (
(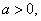
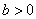
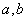 是常数)是否是
是常数)是否是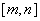 (
(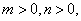
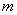 、
、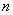 是常数)上的有
是常数)上的有
界函数?
(I)解法1:∵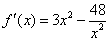 ,由
,由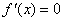 得
得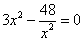 ,
,
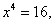 ∵
∵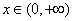 , ∴
, ∴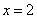 ,
,
∵当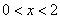 时,
时,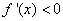 ,∴函数
,∴函数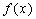 在(0,2)上是减函数;
在(0,2)上是减函数;
当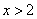 时,
时,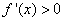 ,∴函数
,∴函数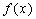 在(2,+
在(2,+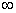 )上是增函数;
)上是增函数;
∴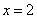 是函数的在区间(0,+
是函数的在区间(0,+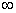 )上的最小值点,
)上的最小值点,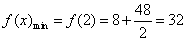
∴对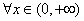 ,都有
,都有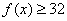 ,
,
即在区间(0,+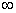 )上存在常数A=32,使得对
)上存在常数A=32,使得对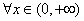 都有
都有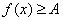 成立,
成立,
∴函数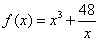 在(0,+
在(0,+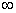 )上有下界.
)上有下界.
[解法2: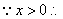
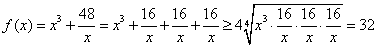
当且仅当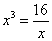 即
即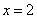 时“=”成立
时“=”成立
∴对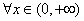 ,都有
,都有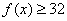 ,
,
即在区间(0,+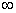 )上存在常数A=32,使得对
)上存在常数A=32,使得对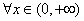 都有
都有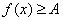 成立,
成立,
∴函数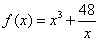 在(0,+
在(0,+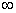 )上有下界.]
)上有下界.]
(II)类比函数有下界的定义,函数有上界可以这样定义:
定义在D上的函数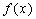 ,如果满足:对
,如果满足:对 ,
,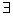 常数B,都有
常数B,都有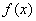 ≤B成立,则称函数
≤B成立,则称函数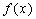 在D上有上界,其中B称为函数的上界.
在D上有上界,其中B称为函数的上界.
设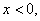
 则
则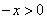 ,由(1)知,对
,由(1)知,对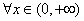 ,都有
,都有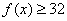 ,
,
∴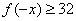 ,∵函数
,∵函数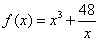 为奇函数,∴
为奇函数,∴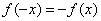
∴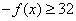 ,∴
,∴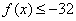
即存在常数B=-32,对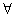
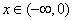 ,都有
,都有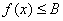 ,
,
∴函数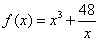 在(-
在(-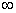 , 0)上有上界.
, 0)上有上界.
(III)∵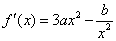 ,
,
由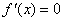 得
得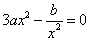 ,∵
,∵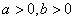

∴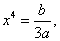 ∵
∵ 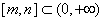 , ∴
, ∴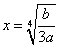 ,
,
∵当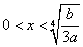 时,
时,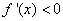 ,∴函数
,∴函数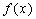 在(0,
在(0,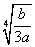 )上是减函数;
)上是减函数;
当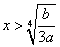 时,
时,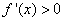 ,∴函数
,∴函数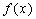 在(
在(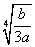 ,+
,+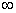 )上是增函数;
)上是增函数;
∴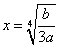 是函数的在区间(0,+
是函数的在区间(0,+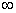 )上的最小值点,
)上的最小值点,
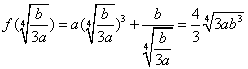
①当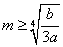 时,函数
时,函数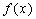 在
在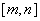 上是增函数;
上是增函数;
∴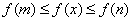
∵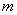 、
、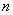 是常数,∴
是常数,∴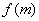 、
、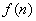 都是常数
都是常数
令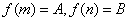 ,
,
∴对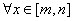 ,
,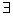 常数A,B,都有
常数A,B,都有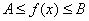
即函数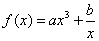 在
在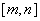 上既有上界又有下界
上既有上界又有下界
②当 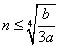 时函数
时函数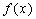 在
在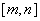 上是减函数
上是减函数
∴对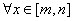 都有
都有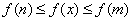
∴函数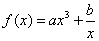 在
在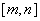 上有界.
上有界.
③当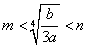 时,函数
时,函数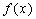 在
在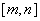 上有最小值
上有最小值
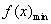 =
=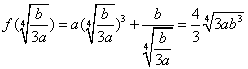
令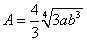 ,令B=
,令B=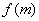 、
、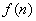 中的最大者
中的最大者
则对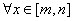 ,
,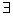 常数A,B,都有
常数A,B,都有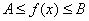
∴函数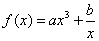 在
在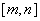 上有界.
上有界.
综上可知函数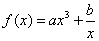 是
是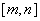 上的有界函数.
上的有界函数.

 阅读快车系列答案
阅读快车系列答案 ⊥平面
⊥平面 ,直线
,直线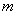
 平面
平面 ,下面有三个命题:①
,下面有三个命题:①
 上异于O的两点,且
上异于O的两点,且 ,则
,则 的最小值为
的最小值为 的值为 .
的值为 . ,若
,若 与
与 的夹角为锐角,则x的范围是____________。
的夹角为锐角,则x的范围是____________。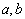 是两条不重合的直线,
是两条不重合的直线,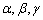 是三个两两不重合的平面,给出下列四个命题:
是三个两两不重合的平面,给出下列四个命题: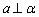 ,
,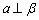 ,则
,则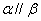 ②若
②若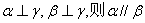
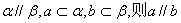 ④若
④若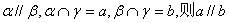
 中,
中, ,
, ,当
,当 时,
时, 等于
等于 的个位数,若数列
的个位数,若数列 项和为243,则
项和为243,则 的焦距为2,以O为圆心,
的焦距为2,以O为圆心,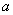 为半径的圆,过点
为半径的圆,过点 作圆的两切线互相垂直,则离心率
作圆的两切线互相垂直,则离心率 = 。
= 。