题目内容
13.已知点A(-1,1),B(3,3)是圆C的一条直径的两个端点,又点M在圆C上运动,点N(4,-2),求线段MN的中点P的轨迹方程.分析 求出圆C的方程,利用代入法,求出线段MN的中点P的轨迹方程.
解答 解:由题意,AB的中点C(1,2),AC=$\sqrt{(1+1)^{2}+(2-1)^{2}}$=$\sqrt{5}$,
∴圆C:(x-1)2+(y-2)2=5,
设P(x,y),则M(2x-4,2y+2),
∵点M在圆C上运动,
∴(2x-4-1)2+(2y+2-2)2=5,
即(x-2.5)2+y2=1.25.
点评 本题考查圆的方程,考查代入法的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
4.已知某几何体的三视图如图所示,则该几何体的表面积为( )
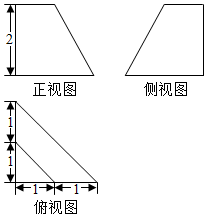

| A. | $\frac{7}{3}$ | B. | $\frac{17}{2}$ | C. | 13 | D. | $\frac{17+3\sqrt{10}}{2}$ |
1.在△ABC中,若a=$\sqrt{3}$,b=1,c=2,则△ABC的面积等于( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{6}+\sqrt{2}}{2}$ |
18.已知sin(θ+$\frac{π}{2}$)<0,cos(θ-$\frac{π}{2}$)>0,则下列不等式关系必定成立的是( )
| A. | tan2$\frac{θ}{2}$<1 | B. | tan2$\frac{θ}{2}$>1 | C. | sin$\frac{θ}{2}$>cos$\frac{θ}{2}$ | D. | sin$\frac{θ}{2}$<cos$\frac{θ}{2}$ |
5.函数y=$\root{3}{{x}^{2}}$-x2+2的图象在以点(1,y1)为切点的切线与坐标轴所围成的三角形面积等于( ),函数y=x3图象上过点(1,y2)的切线与两条坐标轴所围成的三角形面积等于( )
| A. | $\frac{25}{6}$ | B. | $\frac{2}{3}$ | C. | $\frac{2}{3}$或$\frac{1}{24}$ | D. | $\frac{15}{4}$ | ||||
| E. | $\frac{7}{3}$ | F. | $\frac{15}{4}$或$\frac{7}{3}$ |
5.下面各组函数中为相同函数的是( )
| A. | f(x)=$\sqrt{(x-1)^{2}}$,g(x)=x-1 | B. | f(x)=$\sqrt{{x}^{2}-1}$,g(x)=$\sqrt{x+1}$•$\sqrt{x-1}$ | ||
| C. | f(x)=ln ex与g(x)=elnx | D. | f(x)=(x-1)0与g(x)=$\frac{1}{(x-1)^{0}}$ |
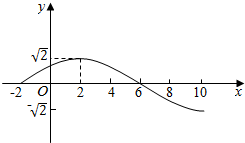 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则f(x)=$\sqrt{2}$sin($\frac{π}{8}$x+$\frac{π}{4}$).
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则f(x)=$\sqrt{2}$sin($\frac{π}{8}$x+$\frac{π}{4}$).