题目内容
8.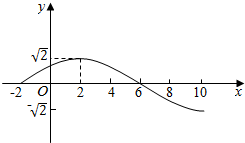 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则f(x)=$\sqrt{2}$sin($\frac{π}{8}$x+$\frac{π}{4}$).
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则f(x)=$\sqrt{2}$sin($\frac{π}{8}$x+$\frac{π}{4}$).
分析 由题意易得A值和周期,可得ω,代入点的坐标计算可得φ值,可得解析式.
解答 解:由题意可得A=$\sqrt{2}$,周期T=$\frac{2π}{ω}$=2[6-(-2)],
解得ω=$\frac{π}{8}$,∴f(x)=$\sqrt{2}$sin($\frac{π}{8}$x+φ),
由函数图象过点(-2,0)可得0=$\sqrt{2}$sin(-$\frac{π}{4}$+φ),
∴-$\frac{π}{4}$+φ=kπ,k∈Z,由|φ|<$\frac{π}{2}$可得φ=$\frac{π}{4}$
故函数的解析式为f(x)=$\sqrt{2}$sin($\frac{π}{8}$x+$\frac{π}{4}$)
故答案为:$\sqrt{2}$sin($\frac{π}{8}$x+$\frac{π}{4}$)
点评 本题考查三角函数的图象和解析式,属基础题.

练习册系列答案
相关题目
3.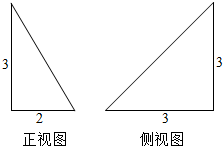 已知一个三棱锥的正视图,侧视图均为直角三角形,其形状及尺寸如图,则该三棱锥的俯视图的面积为( )
已知一个三棱锥的正视图,侧视图均为直角三角形,其形状及尺寸如图,则该三棱锥的俯视图的面积为( )
 已知一个三棱锥的正视图,侧视图均为直角三角形,其形状及尺寸如图,则该三棱锥的俯视图的面积为( )
已知一个三棱锥的正视图,侧视图均为直角三角形,其形状及尺寸如图,则该三棱锥的俯视图的面积为( )| A. | 3 | B. | 6 | C. | $\frac{9}{2}$或9 | D. | 3或6 |
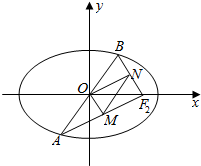 已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点为F2(1,0),且经过点(1,-$\frac{3}{2}$).
已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点为F2(1,0),且经过点(1,-$\frac{3}{2}$).