题目内容
5.函数y=$\root{3}{{x}^{2}}$-x2+2的图象在以点(1,y1)为切点的切线与坐标轴所围成的三角形面积等于( ),函数y=x3图象上过点(1,y2)的切线与两条坐标轴所围成的三角形面积等于( )| A. | $\frac{25}{6}$ | B. | $\frac{2}{3}$ | C. | $\frac{2}{3}$或$\frac{1}{24}$ | D. | $\frac{15}{4}$ | ||||
| E. | $\frac{7}{3}$ | F. | $\frac{15}{4}$或$\frac{7}{3}$ |
分析 求出函数y=$\root{3}{{x}^{2}}$-x2+2的导数,求得切线的斜率和切点,由点斜式方程可得切线的方程,再令x=0,y=0,求得与坐标轴的交点,可得三角形的面积;
求得函数y=x3的导数,设出切点,求得切线的斜率,写出切线的方程,代入点(1,1),求得切线的斜率,可得切线的方程,令x=0,y=0,求出与坐标轴的交点,计算三角形的面积即可.
解答 解:函数y=$\root{3}{{x}^{2}}$-x2+2的导数为y′=$\frac{2}{3}$•${x}^{-\frac{1}{3}}$-2x,
以点(1,y1)为切点的切线斜率为$\frac{2}{3}$-2=-$\frac{4}{3}$,
切点为(1,2),
可得以点(1,y1)为切点的切线方程为y-2=-$\frac{4}{3}$(x-1),
令x=0,可得y=$\frac{10}{3}$;令y=0,可得x=$\frac{5}{2}$.
则切线与坐标轴所围成的三角形面积等于$\frac{1}{2}$•$\frac{10}{3}$•$\frac{5}{2}$=$\frac{25}{6}$,
故选:A;
函数y=x3的导数为y′=3x2,设切点为(m,m3),
即有切线的斜率为3m2,
切线的方程为y-m3=3m2(x-m),
由y2=1,代入点(1,1),可得
2m3-3m2+1=0,即为(m-1)2(2m+1)=0,
解得m=1或-$\frac{1}{2}$,
由m=1,可得切线的方程为y-1=3(x-1),
由x=0,解得y=-2;y=0,可得x=$\frac{2}{3}$.
即有所求三角形的面积为$\frac{1}{2}$•2•$\frac{2}{3}$=$\frac{2}{3}$;
由m=-$\frac{1}{2}$,可得y-1=$\frac{3}{4}$(x-1),
由x=0,解得y=$\frac{1}{4}$;y=0,可得x=-$\frac{1}{3}$.
即有所求三角形的面积为$\frac{1}{2}$•$\frac{1}{4}$•$\frac{1}{3}$=$\frac{1}{24}$.
即有切线与两条坐标轴所围成的三角形面积为$\frac{2}{3}$或$\frac{1}{24}$.
故选:C.
点评 本题考查导数的运用:求切线的方程,考查导数的几何意义,考查三角形的面积的求法,属于中档题和易错题.

 金钥匙试卷系列答案
金钥匙试卷系列答案| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{5}-1}{2}$ |
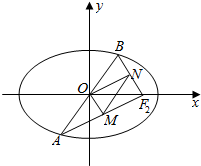 已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点为F2(1,0),且经过点(1,-$\frac{3}{2}$).
已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点为F2(1,0),且经过点(1,-$\frac{3}{2}$).