题目内容
4．已知某几何体的三视图如图所示，则该几何体的表面积为（ ）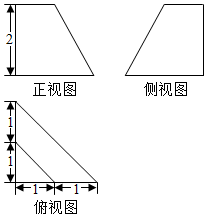
| A． | $\frac{7}{3}$ | B． | $\frac{17}{2}$ | C． | 13 | D． | $\frac{17+3\sqrt{10}}{2}$ |
分析 几何体为三棱台，其中两个侧面和底面垂直，上下底为直角三角形．利用勾股定理求出斜高．
解答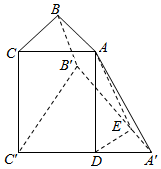 
解由三视图可知几何体为三棱台，作出直观图如图所示，
则CC′⊥平面ABC，上下底均为等腰直角三角形，AC⊥BC，AC=BC=1，A′C′=B′C′=C′C=2，∴AB=$\sqrt{2}$，A′B′=2$\sqrt{2}$．
∴棱台的上底面积为$\frac{1}{2}×1×1$=$\frac{1}{2}$，下底面积为$\frac{1}{2}×2×2$=2，梯形ACC′A′的面积为$\frac{1}{2}×$（1+2）×2=3，
梯形BCC′B′的面积为$\frac{1}{2}×（1+2）×2$=3，
过A作AD⊥A′C′于D，过D作DE⊥A′B′，则AD=CC′=2，DE为△A′B′C′斜边高的$\frac{1}{2}$，
∴DE=$\frac{\sqrt{2}}{2}$，∴AE=$\sqrt{A{D}^{2}+D{E}^{2}}$=$\frac{3}{\sqrt{2}}$．∴梯形ABB′A′的面积为$\frac{1}{2}×$（$\sqrt{2}+2\sqrt{2}$）×$\frac{3}{\sqrt{2}}$=$\frac{9}{2}$．
∴几何体的表面积S=$\frac{1}{2}+2$$+3+3+\frac{9}{2}$=13．
故选：C．
点评 本题考查了棱台的结构特征和三视图，面积计算，属于中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
15．己知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的右焦点为F，右顶点和上顶点分别为A、B，过点F作x轴的垂线与椭圆在第一象限于点P，直线OP交AB于点Q，若|OQ|=|AQ|，则椭圆的离心率为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{\sqrt{2}}{2}$ | C． | $\frac{\sqrt{3}}{2}$ | D． | $\frac{\sqrt{5}-1}{2}$ |
12．若$\overrightarrow{a}$=（2，-1），$\overrightarrow{b}$=（x，2）且$\overrightarrow{a}$⊥（$\overrightarrow{a}$+$\overrightarrow{b}$），则x等于（ ）
| A． | -$\frac{1}{2}$ | B． | $\frac{1}{2}$ | C． | -$\frac{3}{2}$ | D． | $\frac{3}{2}$ |
9．已知向量$\overrightarrow{a}$，$\overrightarrow{b}$，则下列关系正确的是（ ）
| A． | |$\overrightarrow{a}•\overrightarrow{b}$|=|$\overrightarrow{a}$||$\overrightarrow{b}$| | B． | |$\overrightarrow{a}•\overrightarrow{b}$|≤|$\overrightarrow{a}$||$\overrightarrow{b}$| | ||
| C． | |$\overrightarrow{a}•\overrightarrow{b}$|≥|$\overrightarrow{a}$||$\overrightarrow{b}$| | D． | 以上答案都不正确 |