题目内容
2.已知A,B∈[-$\frac{π}{2}$,$\frac{π}{2}$],且cosA+cosB=cosAcosB,则sin(A-B)的值为0.分析 由已知可得(cosA-1)(cosB-1)=1,结合范围A,B∈[-$\frac{π}{2}$,$\frac{π}{2}$],可得cosA,cosB∈[0,1],从而求得cosA=cosB=0,利用两角差的正弦函数公式即可求值得解.
解答 解:∵cosA+cosB=cosAcosB,
∴(cosA-1)(cosB-1)=1,
∵A,B∈[-$\frac{π}{2}$,$\frac{π}{2}$],
∴cosA,cosB∈[0,1],
∴cosA=cosB=0,
∴sin(A-B)=sinAcosB-cosAsinB=0.
故答案为:0.
点评 本题主要考查了两角差的正弦函数公式,余弦函数的图象和性质的综合应用,考查了转化思想,技巧性较强,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.若$\overrightarrow{a}$=(2,-1),$\overrightarrow{b}$=(x,2)且$\overrightarrow{a}$⊥($\overrightarrow{a}$+$\overrightarrow{b}$),则x等于( )
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{3}{2}$ | D. | $\frac{3}{2}$ |
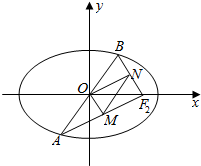 已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点为F2(1,0),且经过点(1,-$\frac{3}{2}$).
已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点为F2(1,0),且经过点(1,-$\frac{3}{2}$).