题目内容
10.已知等比数列{an}的公比q=2,a4=8,Sn为{an}的前n项和,设a=a20.3,b=0.3${\;}^{{a}_{3}}$,c=logan(Sn+$\frac{1}{{S}_{n}}$),则a,b,c大小关系是( )| A. | a<b<c | B. | b<a<c | C. | c<b<a | D. | b<c<a |
分析 由等比数列的性质得a1=1,an=1×2n-1=2n-1,a2=2,a3=4,${S}_{n}=\frac{1-{2}^{n}}{1-2}$=2n-1,由此利用对数函数和指数函数的单调性质能判断a,b,c的大小关系.
解答 解:∵等比数列{an}的公比q=2,a4=8,Sn为{an}的前n项和,
∴${a}_{4}={a}_{1}{q}^{3}$,∴8=a1•8,
解得a1=1,∴an=1×2n-1=2n-1,
∴a2=2,a3=4,${S}_{n}=\frac{1-{2}^{n}}{1-2}$=2n-1,
设a=a20.3,b=0.3${\;}^{{a}_{3}}$,c=logan(Sn+$\frac{1}{{S}_{n}}$),
∴a=20.3∈(1,$\sqrt{2}$),a=20.3<20.5=$\sqrt{2}$,b=0.34∈(0,1),
∵n∈N*,∴1≤2n-1≤2n-1,
∴$\sqrt{2}$<c=$lo{g}_{{2}^{n-1}}({2}^{n}-1+\frac{1}{{2}^{n}-1})$<2,
∴a,b,c大小关系是b<a<c.
故选:B.
点评 本题考查等比数列的前5项和的求法,是中档题,解题时要认真审题,注意等差数列、等比数列的性质的合理运用.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
1. 运行下列程序,当输入数值-2时,输出结果是( )
运行下列程序,当输入数值-2时,输出结果是( )
 运行下列程序,当输入数值-2时,输出结果是( )
运行下列程序,当输入数值-2时,输出结果是( )| A. | 7 | B. | 3 | C. | 0 | D. | -16 |
18.已知函数f(x)=log2(x2-2x-3),则下列各区间中,能满足f(x)单调递减的是( )
| A. | (3,6) | B. | (1,2) | C. | (-1,3) | D. | (-∞,-1) |
15.若$tan({α+\frac{π}{4}})<0$,则下列结论正确的是( )
| A. | sinα>0 | B. | cosα>0 | C. | sin2α<0 | D. | cos2α<0 |
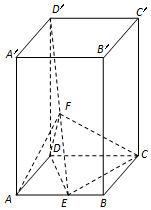 如图,底面为平行四边形的四棱柱ABCD-A'B'C'D'中,DD'⊥平面ABCD,∠DAB=$\frac{π}{3}$,AB=2AD,DD'=3AD,E、F分别是线段AB、D'E的中点.
如图,底面为平行四边形的四棱柱ABCD-A'B'C'D'中,DD'⊥平面ABCD,∠DAB=$\frac{π}{3}$,AB=2AD,DD'=3AD,E、F分别是线段AB、D'E的中点.