题目内容
两个非零向量
与
满足|
|=4，|
|=2，且
与
夹角为60°．
（1）求
•
；
（2）|
+
|．
| a |
| b |
| a |
| b |
| a |
| b |
（1）求
| a |
| b |
（2）|
| a |
| b |
考点：数量积表示两个向量的夹角,向量的模,平面向量数量积的运算
专题：平面向量及应用
分析：（1）根据数量积的计算公式即可求出
•
；
（2）根据向量的模的平方等于向量的平方，所以|
+
|=
=
，所以根据条件求(
+
)2即可．
| a |
| b |
（2）根据向量的模的平方等于向量的平方，所以|
| a |
| b |
|
|
(
|
| a |
| b |
解答：
解：（1）
•
=|
||
|cos60°=4；
（2）|
+
|=
=
=
=2
．
| a |
| b |
| a |
| b |
（2）|
| a |
| b |
(
|
|
| 16+4+8 |
| 7 |
点评：考查向量数量积的计算公式以及求向量长度的方法．
练习册系列答案
阅读快车系列答案
相关题目
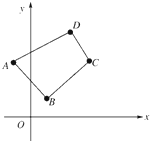已知四点坐标：A（-1，3），B（1，1），C（4，4），D（3，5）．