题目内容
点B是半径为4的圆O内一定点，BO=2，动点A在圆O上，当∠BAO最大时，
•
= ．
| AB |
| AO |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：建系，∠BAO即为向量
与向量
的夹角，又动点A在圆O上可得当A为（0，-4）时，∠BAO=π最大，求解向量的坐标可得数量积．
| AO |
| AB |
解答：
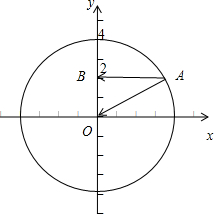解：由题意建立如图所示的坐标系，可得O（0，0），B（0，2），
∠BAO即为向量
与向量
的夹角，又动点A在圆O上
可得当A为（0，-4）时，∠BAO=π最大，
此时
=（0，0）-（0，-4）=（0，4），
=（0，2）-（0，-4）=（0，6），
∴
•
=0×0+4×6=24
故答案为：24
解：由题意建立如图所示的坐标系，可得O（0，0），B（0，2），∠BAO即为向量
| AO |
| AB |
可得当A为（0，-4）时，∠BAO=π最大，
此时
| AO |
| AB |
∴
| AB |
| AO |
故答案为：24
点评：本题考查平面向量数量积的运算，建系并得出去最值时的点A是解决问题的关键，属中档题．
练习册系列答案
计算高手系列答案
相关题目
已知α为锐角，cos（α+
）=
，则sinα=（ ）
| π |
| 6 |
| 2 |
| 3 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|