题目内容
16.已知数列{an}的前n项和,${S_n}=\frac{{3{n^2}-n}}{2}$.(1)求{an}的通项公式;
(2)设${b_n}=\frac{1}{{{a_n}{a_{n+1}}}}$,数列{bn}的前n项和为Tn,若对?n∈N*,t≤4Tn恒成立,求实数t的最大值.
分析 (1)分类讨论:n=1时,a1=S1;n≥2时,an=Sn-Sn-1;
(2)利用裂项相消法求和,然后根据t≤4Tn恒成立来求t的最大值.
解答 解:∵数列{an}的前n项和,${S_n}=\frac{{3{n^2}-n}}{2}$,
∴a1=S1=1,
n≥2时,Sn-Sn-1=$\frac{3{n}^{2}-n}{2}$-$\frac{3(n-1)^{2}-(n-1)}{2}$=3n-2,
n=1时,上式成立,
∴an=3n-2.
(2)由an=3n-2,可得${b_n}=\frac{1}{{{a_n}{a_{n+1}}}}=\frac{1}{{({3n-2})({3n+1})}}=\frac{1}{3}({\frac{1}{3n-2}-\frac{1}{3n+1}}),{T_n}={b_1}+{b_2}+…+{b_n}$=$\frac{1}{3}[{({1-\frac{1}{4}})+({\frac{1}{4}-\frac{1}{7}})+…+({\frac{1}{3n-2}-\frac{1}{3n+1}})}]=\frac{n}{3n+1}$.
因为${T_{n+1}}-{T_n}=\frac{n+1}{{3({n+1})+1}}-\frac{n}{3n+1}=\frac{1}{{({3n+1})({3n+4})}}>0$,
所以Tn+1>Tn,所以数列{Tn}是递增数列.
所以$t≤4{T_n}?\frac{t}{4}≤{T_n}?\frac{t}{4}≤{T_1}=\frac{1}{4}?t≤1$,
所以实数t的最大值是1.
点评 本题主要考查了利用数列的递推公式构造等差数列求数列的通项公式,及数列的裂项求和方法的应用及恒成立与最值求解的应用.

练习册系列答案
相关题目
6.准线方程是y=-2的抛物线标准方程是( )
| A. | x2=8y | B. | x2=-8y | C. | y2=-8x | D. | y2=8x |
4.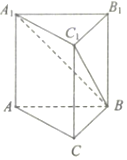 《九章九术》是我国古代数学名著,它在几何学中的研究比西方早一千多年.例如堑堵指底面为直角三角形,且侧棱垂直于底面的三棱柱;阳马指底面为矩形,一侧棱垂直于底面的四棱锥.如图,在堑堵ABC-A1B1C1中,AC⊥BC,若A1A=AB=2,当阳马B-A1ACC1体积最大时,则堑堵ABC-A1B1C1的体积为( )
《九章九术》是我国古代数学名著,它在几何学中的研究比西方早一千多年.例如堑堵指底面为直角三角形,且侧棱垂直于底面的三棱柱;阳马指底面为矩形,一侧棱垂直于底面的四棱锥.如图,在堑堵ABC-A1B1C1中,AC⊥BC,若A1A=AB=2,当阳马B-A1ACC1体积最大时,则堑堵ABC-A1B1C1的体积为( )
 《九章九术》是我国古代数学名著,它在几何学中的研究比西方早一千多年.例如堑堵指底面为直角三角形,且侧棱垂直于底面的三棱柱;阳马指底面为矩形,一侧棱垂直于底面的四棱锥.如图,在堑堵ABC-A1B1C1中,AC⊥BC,若A1A=AB=2,当阳马B-A1ACC1体积最大时,则堑堵ABC-A1B1C1的体积为( )
《九章九术》是我国古代数学名著,它在几何学中的研究比西方早一千多年.例如堑堵指底面为直角三角形,且侧棱垂直于底面的三棱柱;阳马指底面为矩形,一侧棱垂直于底面的四棱锥.如图,在堑堵ABC-A1B1C1中,AC⊥BC,若A1A=AB=2,当阳马B-A1ACC1体积最大时,则堑堵ABC-A1B1C1的体积为( )| A. | $\frac{8}{3}$ | B. | $\sqrt{2}$ | C. | 2 | D. | $2\sqrt{2}$ |
1.已知空间两点A(3,3,1),B(-1,1,5),则线段AB的长度为( )
| A. | 6 | B. | $2\sqrt{6}$ | C. | $4\sqrt{3}$ | D. | $2\sqrt{14}$ |