题目内容
7.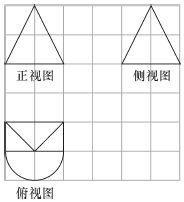 如图,网格纸上正方形的边长为1,图中粗实线画出的是一个几何体的三视图,则这个几何体的表面积是( )
如图,网格纸上正方形的边长为1,图中粗实线画出的是一个几何体的三视图,则这个几何体的表面积是( )| A. | $({1+\frac{{\sqrt{5}}}{2}})•π+2({1+\sqrt{5}})$ | B. | $\frac{{({1+\sqrt{5}})}}{2}•π+2({1+\sqrt{5}})$ | C. | $\frac{{({1+\sqrt{5}})}}{2}•π+2({3+\sqrt{5}})$ | D. | $\frac{{({1+\sqrt{5}})}}{2}•π+4+\sqrt{5}$ |
分析 由三视图可知,该几何体是底面为矩形的直四棱锥与半个圆锥的组合体,利用所给数据,即可求出其表面积.
解答 解:由三视图可知,该几何体是底面为矩形的直四棱锥与半个圆锥的组合体,
表面积是$\frac{1}{2}π$+2+$\frac{1}{2}•$$π•1•\sqrt{5}$+2×$\frac{1}{2}×1×\sqrt{5}$+$\frac{1}{2}×2×\sqrt{5}$=$\frac{(1+\sqrt{5})}{2}π$+2(1+$\sqrt{5}$),
故选B.
点评 本题考查了利用空间几何体的三视图求几何体的体积的应用问题,是基础题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.点P为棱长是$2\sqrt{5}$的正方体ABCD-A1B1C1D1的内切球O球面上的动点,点M为B1C1的中点,若满足DP⊥BM,则动点P的轨迹的长度为( )
| A. | π | B. | 2π | C. | 4π | D. | $2\sqrt{5}π$ |
12.已知定义域为R的奇函数f(x)满足f(x+1)=f(3-x),当x∈(0,2]时,f(x)=-x2+4,则函数y=f(x)-a(a∈R)在区间[-4,8]上的零点个数最多时,所有零点之和为14.
19.已知集合A={3a,3},B={a2+2a,4},A∩B={3},则A∪B等于( )
| A. | {3,5} | B. | {3,4} | C. | {-9,3} | D. | {-9,3,4} |
16.已知函数f(x)=(x2+x-1)ex,则曲线y=f(x)在点(1,f(1))处的切线方程为( )
| A. | y=3ex-2e | B. | y=3ex-4e | C. | y=4ex-5e | D. | y=4ex-3e |
17.i为虚数单位,若$\frac{a+bi}{i}$(a,b∈R)与(2-i)2互为共轭复数,则a-b=( )
| A. | 1 | B. | -1 | C. | 7 | D. | -7 |