题目内容
16．已知函数f（x）=（x2+x-1）ex，则曲线y=f（x）在点（1，f（1））处的切线方程为（ ）| A． | y=3ex-2e | B． | y=3ex-4e | C． | y=4ex-5e | D． | y=4ex-3e |
分析 求出函数的导数，求出切线的斜率，切点坐标，然后求解切线方程．
解答 解：函数f（x）=（x2+x-1）ex，可得：f′（x）=（x2+3x）ex，
则f′（1）=4e，f（1）=e；
曲线y=f（x）在点（1，f（1））处的切线方程为：y=4ex-3e．
故选：D．
点评 本题考查切线方程的求法，考查计算能力．
练习册系列答案
相关题目
6．已知二元一次方程组的增广矩阵为$（\begin{array}{l}{m}&{4}&{m+2}\\{1}&{m}&{m}\end{array}）$，若此方程组无实数解，则实数m的值为（ ）
| A． | m=±2 | B． | m=2 | C． | m=-2 | D． | m≠±2 |
7．
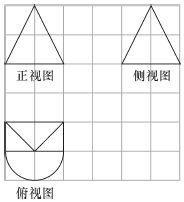如图，网格纸上正方形的边长为1，图中粗实线画出的是一个几何体的三视图，则这个几何体的表面积是（ ）
如图，网格纸上正方形的边长为1，图中粗实线画出的是一个几何体的三视图，则这个几何体的表面积是（ ）| A． | $（{1+\frac{{\sqrt{5}}}{2}}）•π+2（{1+\sqrt{5}}）$ | B． | $\frac{{（{1+\sqrt{5}}）}}{2}•π+2（{1+\sqrt{5}}）$ | C． | $\frac{{（{1+\sqrt{5}}）}}{2}•π+2（{3+\sqrt{5}}）$ | D． | $\frac{{（{1+\sqrt{5}}）}}{2}•π+4+\sqrt{5}$ |
8．
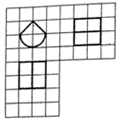如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，其中曲线部分是圆弧，则此几何体的表面积为（ ）
如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，其中曲线部分是圆弧，则此几何体的表面积为（ ）| A． | 2+4$\sqrt{2}$+3π | B． | 2+4$\sqrt{2}$+5π | C． | 10+π | D． | 20+2π |
5．设a=0.30.1，b=log${\;}_{\frac{1}{3}}$$\frac{1}{5}$，c=log425，则a，b，c的大小关系是（ ）
| A． | a＞b＞c | B． | a＞c＞b | C． | b＞c＞a | D． | c＞b＞a |
6．设实数x、y满足$\left\{\begin{array}{l}{2x+y≥4}\\{x-y≥-1}\\{x-2y≤2}\end{array}\right.$，则z=x+y为（ ）
| A． | 有最小值2，无最大值 | B． | 有最小值2，最大值3 | ||
| C． | 有最大值3，无最小值 | D． | 既无最小值，也无最大值 |