题目内容
2.我国古代数学典籍《九章算术》第七章“盈不足”中有一道两鼠穿墙问题:“今有垣厚五尺,两鼠对穿,大鼠日一尺,小鼠日一尺,大鼠日自倍,小鼠日自半,问何日相逢,各穿几何”,翻译过来就是:有五尺厚的墙,两只老鼠从墙的两边相对分别打洞穿墙,大、小鼠第一天都进一尺,以后每天,大鼠加倍,小鼠减半,则几天后两鼠相遇,这个问题体现了古代对数列问题的研究,现将墙的厚度改为500尺,则需要几天时间才能打穿(结果取整数)( )| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
分析 设需要n天时间才能打穿,则$\frac{{2}^{n}-1}{2-1}$+$\frac{1-(\frac{1}{2})^{n}}{1-\frac{1}{2}}$≥500,化为:2n-$\frac{2}{{2}^{n}}$-499≥0,令f(n)=2n-$\frac{2}{{2}^{n}}$-499,f(x)=${2}^{x}-\frac{2}{{2}^{x}}$-499,(x≥1).利用函数零点存在定理与函数的单调性即可得出.
解答 解:设需要n天时间才能打穿,则$\frac{{2}^{n}-1}{2-1}$+$\frac{1-(\frac{1}{2})^{n}}{1-\frac{1}{2}}$≥500,
化为:2n-$\frac{2}{{2}^{n}}$-499≥0,
令f(n)=2n-$\frac{2}{{2}^{n}}$-499,则f(8)=${2}^{8}-\frac{2}{{2}^{8}}$-499=-$\frac{1}{{2}^{7}}$-243<0.
f(9)=29-$\frac{2}{{2}^{9}}$-499=13-$\frac{1}{{2}^{8}}$>0.
f(x)=${2}^{x}-\frac{2}{{2}^{x}}$-499,(x≥1).
∴f(x)在(8,9)内存在一个零点.
又函数f(x)在x≥1时单调递增,因此f(x)在(8,9)内存在唯一一个零点.
∴需要9天时间才能打穿.
故选:D.
点评 本题考查了函数零点存在定理与函数的单调性、等比数列的通项公式与求和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
12.一物体A以速度v(t)=t2-t+6沿直线运动,则当时间由t=1变化到t=4时,物体A运动的路程是( )
| A. | 26.5 | B. | 53 | C. | 31.5 | D. | 63 |
13.某三棱锥的三视图如图所示,则该三棱锥的表面积是( )


| A. | $2+\sqrt{5}$ | B. | $2+2\sqrt{5}$ | C. | $4+\sqrt{5}$ | D. | 5 |
10. 全世界越来越关注环境保护问题,某省一监测站点于2016年8月某日起连续x天监测空气质量指数(AQI),数据统计如下:
全世界越来越关注环境保护问题,某省一监测站点于2016年8月某日起连续x天监测空气质量指数(AQI),数据统计如下:
(Ⅰ)根据所给统计表和频率分布直方图中的信息求出x、y的值,并完成频率分布直方图;
(Ⅱ)在空气质量指数分别为[50,100)和[150,200)的监测数据中,用分层抽样的方法抽取5天,从中任意选取2天,求事件A“两天空气都为良”发生的概率.
 全世界越来越关注环境保护问题,某省一监测站点于2016年8月某日起连续x天监测空气质量指数(AQI),数据统计如下:
全世界越来越关注环境保护问题,某省一监测站点于2016年8月某日起连续x天监测空气质量指数(AQI),数据统计如下:| 空气质量指数(μg/m3) | [0,50) | [50,100) | [100,150) | [150,200) | [201,250] |
| 空气质量等级 | 空气优 | 空气良 | 轻度污染 | 中度污染 | 重度污染 |
| 天数 | 20 | 40 | y | 10 | 5 |
(Ⅱ)在空气质量指数分别为[50,100)和[150,200)的监测数据中,用分层抽样的方法抽取5天,从中任意选取2天,求事件A“两天空气都为良”发生的概率.
17.若全集U={1,2,3,4,5,6,7},集合A={1,3,5,7},集合B={1,4,7},则集合(∁UA)∩B=( )
| A. | {4} | B. | {1,2,4,6,7} | C. | {3,5} | D. | {1,7} |
7.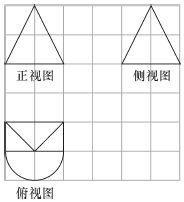 如图,网格纸上正方形的边长为1,图中粗实线画出的是一个几何体的三视图,则这个几何体的表面积是( )
如图,网格纸上正方形的边长为1,图中粗实线画出的是一个几何体的三视图,则这个几何体的表面积是( )
 如图,网格纸上正方形的边长为1,图中粗实线画出的是一个几何体的三视图,则这个几何体的表面积是( )
如图,网格纸上正方形的边长为1,图中粗实线画出的是一个几何体的三视图,则这个几何体的表面积是( )| A. | $({1+\frac{{\sqrt{5}}}{2}})•π+2({1+\sqrt{5}})$ | B. | $\frac{{({1+\sqrt{5}})}}{2}•π+2({1+\sqrt{5}})$ | C. | $\frac{{({1+\sqrt{5}})}}{2}•π+2({3+\sqrt{5}})$ | D. | $\frac{{({1+\sqrt{5}})}}{2}•π+4+\sqrt{5}$ |
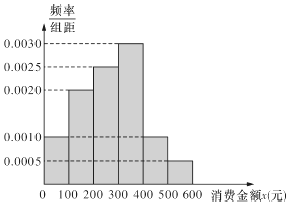 长沙梅溪湖步步高购物中心在开业之后,为了解消费者购物金额的分布,在当月的电脑消费小票中随机抽取n张进行统计,将结果分成6组,分别是:[0,100),[100,200),[200,300),[300,400),[400,500),[500,600],制成如下所示的频率分布直方图(假设消费金额均在[0,600]元的区间内).
长沙梅溪湖步步高购物中心在开业之后,为了解消费者购物金额的分布,在当月的电脑消费小票中随机抽取n张进行统计,将结果分成6组,分别是:[0,100),[100,200),[200,300),[300,400),[400,500),[500,600],制成如下所示的频率分布直方图(假设消费金额均在[0,600]元的区间内). 团购已成为时下商家和顾客均非常青睐的一种省钱、高效的消费方式,不少商家同时加入多家团购网,现恰有三个团购网站在A市开展了团购业务,A市某调查公司为调查这三家团购网站在本市的开展情况,从本市已加入了团购网站的商家中随机地抽取了50家进行调查,他们加入这三家团购网站的情况如下图所示.
团购已成为时下商家和顾客均非常青睐的一种省钱、高效的消费方式,不少商家同时加入多家团购网,现恰有三个团购网站在A市开展了团购业务,A市某调查公司为调查这三家团购网站在本市的开展情况,从本市已加入了团购网站的商家中随机地抽取了50家进行调查,他们加入这三家团购网站的情况如下图所示.