题目内容
19.已知集合A={3a,3},B={a2+2a,4},A∩B={3},则A∪B等于( )| A. | {3,5} | B. | {3,4} | C. | {-9,3} | D. | {-9,3,4} |
分析 利用交集性质求出a=-3,从而求出集合A和B,由此能求出A∪B.
解答 解:∵集合A={3a,3},B={a2+2a,4},A∩B={3},
∴$\left\{\begin{array}{l}{{a}^{2}+2a=3}\\{3a≠3}\end{array}\right.$,解得a=-3,
∴A={-9,3},B={3,4},
A∪B={-9,3,4}.
故选:D.
点评 本题考查交集、并集的求法,是基础题,解题时要认真审题,注意交集、并集定义的合理运用.

练习册系列答案
相关题目
9.方程$\frac{{x}^{2}}{10-m}$+$\frac{{y}^{2}}{m-2}$=1表示焦点在x轴上的椭圆,则m的取值范围为( )
| A. | (2,+∞) | B. | (2,6)∪(6,10) | C. | (2,10) | D. | (2,6) |
10. 全世界越来越关注环境保护问题,某省一监测站点于2016年8月某日起连续x天监测空气质量指数(AQI),数据统计如下:
全世界越来越关注环境保护问题,某省一监测站点于2016年8月某日起连续x天监测空气质量指数(AQI),数据统计如下:
(Ⅰ)根据所给统计表和频率分布直方图中的信息求出x、y的值,并完成频率分布直方图;
(Ⅱ)在空气质量指数分别为[50,100)和[150,200)的监测数据中,用分层抽样的方法抽取5天,从中任意选取2天,求事件A“两天空气都为良”发生的概率.
 全世界越来越关注环境保护问题,某省一监测站点于2016年8月某日起连续x天监测空气质量指数(AQI),数据统计如下:
全世界越来越关注环境保护问题,某省一监测站点于2016年8月某日起连续x天监测空气质量指数(AQI),数据统计如下:| 空气质量指数(μg/m3) | [0,50) | [50,100) | [100,150) | [150,200) | [201,250] |
| 空气质量等级 | 空气优 | 空气良 | 轻度污染 | 中度污染 | 重度污染 |
| 天数 | 20 | 40 | y | 10 | 5 |
(Ⅱ)在空气质量指数分别为[50,100)和[150,200)的监测数据中,用分层抽样的方法抽取5天,从中任意选取2天,求事件A“两天空气都为良”发生的概率.
7.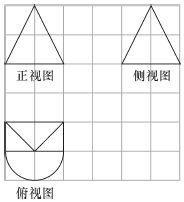 如图,网格纸上正方形的边长为1,图中粗实线画出的是一个几何体的三视图,则这个几何体的表面积是( )
如图,网格纸上正方形的边长为1,图中粗实线画出的是一个几何体的三视图,则这个几何体的表面积是( )
 如图,网格纸上正方形的边长为1,图中粗实线画出的是一个几何体的三视图,则这个几何体的表面积是( )
如图,网格纸上正方形的边长为1,图中粗实线画出的是一个几何体的三视图,则这个几何体的表面积是( )| A. | $({1+\frac{{\sqrt{5}}}{2}})•π+2({1+\sqrt{5}})$ | B. | $\frac{{({1+\sqrt{5}})}}{2}•π+2({1+\sqrt{5}})$ | C. | $\frac{{({1+\sqrt{5}})}}{2}•π+2({3+\sqrt{5}})$ | D. | $\frac{{({1+\sqrt{5}})}}{2}•π+4+\sqrt{5}$ |
8.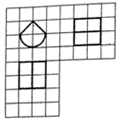 如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,其中曲线部分是圆弧,则此几何体的表面积为( )
如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,其中曲线部分是圆弧,则此几何体的表面积为( )
 如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,其中曲线部分是圆弧,则此几何体的表面积为( )
如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,其中曲线部分是圆弧,则此几何体的表面积为( )| A. | 2+4$\sqrt{2}$+3π | B. | 2+4$\sqrt{2}$+5π | C. | 10+π | D. | 20+2π |
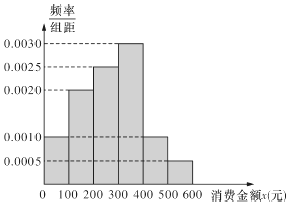 长沙梅溪湖步步高购物中心在开业之后,为了解消费者购物金额的分布,在当月的电脑消费小票中随机抽取n张进行统计,将结果分成6组,分别是:[0,100),[100,200),[200,300),[300,400),[400,500),[500,600],制成如下所示的频率分布直方图(假设消费金额均在[0,600]元的区间内).
长沙梅溪湖步步高购物中心在开业之后,为了解消费者购物金额的分布,在当月的电脑消费小票中随机抽取n张进行统计,将结果分成6组,分别是:[0,100),[100,200),[200,300),[300,400),[400,500),[500,600],制成如下所示的频率分布直方图(假设消费金额均在[0,600]元的区间内).