题目内容
12.已知定义域为R的奇函数f(x)满足f(x+1)=f(3-x),当x∈(0,2]时,f(x)=-x2+4,则函数y=f(x)-a(a∈R)在区间[-4,8]上的零点个数最多时,所有零点之和为14.分析 利用函数的奇偶性以及函数的对称性,画出函数的图象,判断函数y=f(x)-a(a∈R)在区间[-4,8]上的零点个数最多时的位置,求解零点之和.
解答  解:定义域为R的奇函数f(x)满足f(x+1)=f(3-x),
解:定义域为R的奇函数f(x)满足f(x+1)=f(3-x),
函数的图象关于x=2对称,
当x∈(0,2]时,f(x)=-x2+4,在[-4,8]上y=f(x)的图象如图:
函数y=f(x)-a(a∈R)在区间[-4,8]上的零点个数最多7个,图象中的红色点.
零点之和为:-4-2+0+2+4+6+8=14.
故答案为:14.
点评 本题考查函数的零点个数,数形结合,考查转化思想以及计算能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.已知集合A={x|x2-1=0},B={-1,2,5},则A∩B=( )
| A. | {-1,2} | B. | {-1} | C. | {-1,5} | D. | ∅ |
20.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的焦距为4$\sqrt{5}$,渐近线方程为2x±y=0,则双曲线的方程为( )
| A. | $\frac{x^2}{4}-\frac{y^2}{16}=1$ | B. | $\frac{x^2}{16}-\frac{y^2}{4}=1$ | C. | $\frac{x^2}{16}-\frac{y^2}{64}=1$ | D. | $\frac{x^2}{64}-\frac{y^2}{16}=1$ |
7.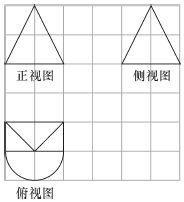 如图,网格纸上正方形的边长为1,图中粗实线画出的是一个几何体的三视图,则这个几何体的表面积是( )
如图,网格纸上正方形的边长为1,图中粗实线画出的是一个几何体的三视图,则这个几何体的表面积是( )
 如图,网格纸上正方形的边长为1,图中粗实线画出的是一个几何体的三视图,则这个几何体的表面积是( )
如图,网格纸上正方形的边长为1,图中粗实线画出的是一个几何体的三视图,则这个几何体的表面积是( )| A. | $({1+\frac{{\sqrt{5}}}{2}})•π+2({1+\sqrt{5}})$ | B. | $\frac{{({1+\sqrt{5}})}}{2}•π+2({1+\sqrt{5}})$ | C. | $\frac{{({1+\sqrt{5}})}}{2}•π+2({3+\sqrt{5}})$ | D. | $\frac{{({1+\sqrt{5}})}}{2}•π+4+\sqrt{5}$ |
2. 如图,将绘有函数f(x)=2sin(ωx+φ)(ω>0,$\frac{π}{2}$<φ<π)的部分图象的纸片沿x轴折成直二面角,若AB之间的空间距离为2$\sqrt{3}$,则f(-1)=( )
如图,将绘有函数f(x)=2sin(ωx+φ)(ω>0,$\frac{π}{2}$<φ<π)的部分图象的纸片沿x轴折成直二面角,若AB之间的空间距离为2$\sqrt{3}$,则f(-1)=( )
 如图,将绘有函数f(x)=2sin(ωx+φ)(ω>0,$\frac{π}{2}$<φ<π)的部分图象的纸片沿x轴折成直二面角,若AB之间的空间距离为2$\sqrt{3}$,则f(-1)=( )
如图,将绘有函数f(x)=2sin(ωx+φ)(ω>0,$\frac{π}{2}$<φ<π)的部分图象的纸片沿x轴折成直二面角,若AB之间的空间距离为2$\sqrt{3}$,则f(-1)=( )| A. | -2 | B. | 2 | C. | -$\sqrt{3}$ | D. | $\sqrt{3}$ |
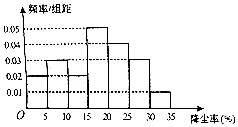 空气质量问题,全民关注,有需求就有研究,某科研团队根据工地常用高压水枪除尘原理,制造了雾霾神器---雾炮,虽然雾炮不能彻底解决问题,但是能在一定程度上起到防霾、降尘的作用,经过测试得到雾炮降尘率的频率分布直方图:
空气质量问题,全民关注,有需求就有研究,某科研团队根据工地常用高压水枪除尘原理,制造了雾霾神器---雾炮,虽然雾炮不能彻底解决问题,但是能在一定程度上起到防霾、降尘的作用,经过测试得到雾炮降尘率的频率分布直方图: