题目内容
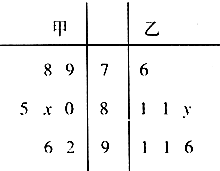 某中学高一年级从甲、乙两个班级各选出7名学生参加学科测试,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生的平均分是85,乙班学生成绩的中位数是83.
某中学高一年级从甲、乙两个班级各选出7名学生参加学科测试,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生的平均分是85,乙班学生成绩的中位数是83.(Ⅰ)求x和y的值,并计算甲班7位学生成绩的方差S2;
(Ⅱ)从成绩在90分以上的学生中随机抽取两名学生,求至少有一名学生是甲班的概率.
考点:列举法计算基本事件数及事件发生的概率,茎叶图,极差、方差与标准差
专题:概率与统计
分析:(Ⅰ)利用平均数求出x的值,中位数求出y的值,根据所给的茎叶图,得出甲班7位学生成绩,做出这7次成绩的平均数,把7次成绩和平均数代入方差的计算公式,求出这组数据的方差.
(Ⅱ)设甲班至少有一名学生为事件A,其对立事件为从成绩在90分以上的学生中随机抽取两名学生,甲班没有一名学生;先计算出从成绩在90分以上的学生中随机抽取两名学生的所有抽取方法总数,和没有甲班一名学生的方法数目,先求出从成绩在90分以上的学生中随机抽取两名学生,甲班没有一名学生的概率,进而结合对立事件的概率性质求得答案.
(Ⅱ)设甲班至少有一名学生为事件A,其对立事件为从成绩在90分以上的学生中随机抽取两名学生,甲班没有一名学生;先计算出从成绩在90分以上的学生中随机抽取两名学生的所有抽取方法总数,和没有甲班一名学生的方法数目,先求出从成绩在90分以上的学生中随机抽取两名学生,甲班没有一名学生的概率,进而结合对立事件的概率性质求得答案.
解答:
解:(Ⅰ)∵甲班学生的平均分是85,设甲班中需求学生的成绩为m,
∴92+96+80+m+85+79+78=85×7,m=85,
∴x=5.
∵乙班学生成绩的中位数是83,∴y=3.
甲班7位学生成绩的方差为S2=
[(-6)2+(-7)2+(-5)2+02+02+72+112]=40.
(Ⅱ)3)甲班成绩在90分以上的学生有两名,分别记为A,B,
乙班成绩在90分以上的学生有三名,分别记为C,D,E,
从这五名学生任意抽取两名学生共有10种情况:
(A,B),(A,C),(A,D),(A,E),(B,C),(B,D),(B,E),(C,D),(C,E),(D,E)
其中甲班至少有一名学生共有7种情况:(A,B),(A,C),(A,D),(A,E),(B,C),(B,D),(B,E).
记“从成绩在90分以上的学生中随机抽取两名学生,甲班至少有一名学生”为事件M,则P(M)=
.
∴92+96+80+m+85+79+78=85×7,m=85,
∴x=5.
∵乙班学生成绩的中位数是83,∴y=3.
甲班7位学生成绩的方差为S2=
| 1 |
| 7 |
(Ⅱ)3)甲班成绩在90分以上的学生有两名,分别记为A,B,
乙班成绩在90分以上的学生有三名,分别记为C,D,E,
从这五名学生任意抽取两名学生共有10种情况:
(A,B),(A,C),(A,D),(A,E),(B,C),(B,D),(B,E),(C,D),(C,E),(D,E)
其中甲班至少有一名学生共有7种情况:(A,B),(A,C),(A,D),(A,E),(B,C),(B,D),(B,E).
记“从成绩在90分以上的学生中随机抽取两名学生,甲班至少有一名学生”为事件M,则P(M)=
| 7 |
| 10 |
点评:本小题主要考查茎叶图、样本均值、样本方差、概率等知识,考查或然与必然的数学思想方法,以及数据处理能力、运算求解能力和应用意识.

练习册系列答案
 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
已知定义域为R的奇函数y=f(x)的导函数为y=f′(x),当x≠0时,f′(x)+
>0,若a=
f(
),b=-2f(-2),c=(ln
)f(ln
),则a,b,c的大小关系正确的是( )
| f(x) |
| x |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| A、a<b<c |
| B、b<c<a |
| C、a<c<b |
| D、c<a<b |
 如图,正四棱锥S-ABCD的底面是边长为a的正方形,侧棱长是底面边长为
如图,正四棱锥S-ABCD的底面是边长为a的正方形,侧棱长是底面边长为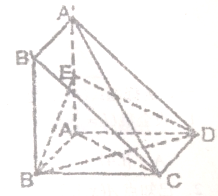 四边形ABCD与A′ABB′都是边长为a的正方形,且平面ABB′A′⊥平面ABCD,点E是A′A的中心.
四边形ABCD与A′ABB′都是边长为a的正方形,且平面ABB′A′⊥平面ABCD,点E是A′A的中心. 根据图示填空:
根据图示填空: