题目内容
已知数列{an}的前n项和为Sn=32n-3.
(1)求数列{an}的通项公式;
(2)设bn=
,求数列{bn}的前n项和Tn.
(1)求数列{an}的通项公式;
(2)设bn=
| n |
| an |
考点:数列的求和,数列递推式
专题:等差数列与等比数列
分析:(1)由Sn=32n-3,利用an=
,能求出an=
.
(2)由bn=
=
,利用分组求和法和错位相减法能求出数列{bn}的前n项和Tn.
|
|
(2)由bn=
| n |
| an |
|
解答:
解:(1)∵已知数列{an}的前n项和为Sn=32n-3,
∴a1=S1=32-3=6,
n≥2时,an=Sn-Sn-1=32n-3-32n-2+3=8•9n-1.
∴an=
.
(2)∵bn=
=
,
∴n=1时,Tn=
,
n≥2时,Tn=
+
+
+…+
,①
Tn=
+
+
+…+
,②
①-②,得
Tn=
+
+
(
+
+…+
)-
=
+
×
-
=
+
-
-
,
∴Tn=
-
-
.
∴Tn=
.
∴a1=S1=32-3=6,
n≥2时,an=Sn-Sn-1=32n-3-32n-2+3=8•9n-1.
∴an=
|
(2)∵bn=
| n |
| an |
|
∴n=1时,Tn=
| 1 |
| 6 |
n≥2时,Tn=
| 1 |
| 6 |
| 2 |
| 8×9 |
| 3 |
| 8×92 |
| n |
| 8×9n-1 |
| 1 |
| 9 |
| 1 |
| 6×9 |
| 2 |
| 8×92 |
| 3 |
| 8×93 |
| n |
| 8×9n |
①-②,得
| 8 |
| 9 |
| 8 |
| 54 |
| 2 |
| 72 |
| 1 |
| 8 |
| 1 |
| 92 |
| 1 |
| 93 |
| 1 |
| 9n-1 |
| n |
| 8×9n |
=
| 19 |
| 108 |
| 1 |
| 8 |
| ||||
1-
|
| n |
| 8×9n |
=
| 19 |
| 108 |
| 1 |
| 64×9 |
| 1 |
| 64×9n |
| n |
| 8×9n |
∴Tn=
| 301 |
| 1536 |
| 1 |
| 512×9n-1 |
| n |
| 64×9n-1 |
∴Tn=
|
点评:本题考查数列的通项公式和前n项和公式的合理运用,是中档题,解题时要认真审题,注意分组求和地和裂项求和法的合理运用.

练习册系列答案
相关题目
已知定义域为R的奇函数y=f(x)的导函数为y=f′(x),当x≠0时,f′(x)+
>0,若a=
f(
),b=-2f(-2),c=(ln
)f(ln
),则a,b,c的大小关系正确的是( )
| f(x) |
| x |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| A、a<b<c |
| B、b<c<a |
| C、a<c<b |
| D、c<a<b |
 如图,正四棱锥S-ABCD的底面是边长为a的正方形,侧棱长是底面边长为
如图,正四棱锥S-ABCD的底面是边长为a的正方形,侧棱长是底面边长为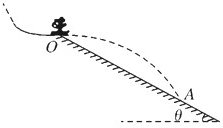 如图,跳台滑雪运动员(可视为质点)经过一段加速滑行后从O点水平飞出,落到斜坡上的A点,已知O点是斜坡的起点,测得A点与O点距离L=12m,斜坡与水平的夹角θ=37°,运动员的质量m=50kg,不计空气阻力,取sin37°=0.60,cos37°=0.80,g取10m/s2.求:
如图,跳台滑雪运动员(可视为质点)经过一段加速滑行后从O点水平飞出,落到斜坡上的A点,已知O点是斜坡的起点,测得A点与O点距离L=12m,斜坡与水平的夹角θ=37°,运动员的质量m=50kg,不计空气阻力,取sin37°=0.60,cos37°=0.80,g取10m/s2.求: