题目内容
设函数f（x）=x|x-2|，x0是函数g（x）=f（f（x））-1的所有零点中的最大值，若x0∈（k，k+1）（k∈Z），则k= ．
考点：函数零点的判定定理
专题：函数的性质及应用
分析：首先，当x∈（0，2）时，利用配方法求最值，然后作函数的图象，故可得f（x0）=1+
，从而由零点的判定定理判断位置．
| 2 |
解答：
解：∵函数f（x）=x|x-2|，
当x∈（0，2）时，
f（x）=x|x-2|=x（2-x）=-（x-1）2+1≤1；
作函数f（x）=x|x-2|的图象如下：
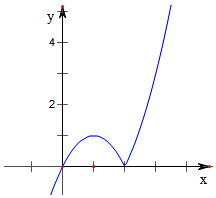
解x（x-2）=1，得到x=1或x=1+
，
又x0是函数g（x）=f（f（x））-1的所有零点中的最大值，
所以f（x0）=1+
，且f（2）=0＜1+
，f（3）=3＞1+
，
因为x0∈（k，k+1）（k∈Z），
所以k=2，
故答案为：2．
当x∈（0，2）时，
f（x）=x|x-2|=x（2-x）=-（x-1）2+1≤1；
作函数f（x）=x|x-2|的图象如下：
解x（x-2）=1，得到x=1或x=1+
| 2 |
又x0是函数g（x）=f（f（x））-1的所有零点中的最大值，
所以f（x0）=1+
| 2 |
| 2 |
| 2 |
因为x0∈（k，k+1）（k∈Z），
所以k=2，
故答案为：2．
点评：本题重点考查函数的基本性质、图象、函数的零点等知识，属于中档题．
练习册系列答案
互动课堂系列答案
激活思维智能训练课时导学练系列答案
相关题目
如图，正四棱锥S-ABCD的底面是边长为a的正方形，侧棱长是底面边长为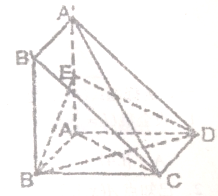
四边形ABCD与A′ABB′都是边长为a的正方形，且平面ABB′A′⊥平面ABCD，点E是A′A的中心．
根据图示填空：