题目内容
若f(2x+1)=x2-4x+2,则f(3-4x)= .
考点:函数解析式的求解及常用方法,函数的值
专题:函数的性质及应用
分析:根据题意,用换元法,设2x+1=t,求出f(t)的解析式,再求f(3-4x)的解析式.
解答:
解:∵f(2x+1)=x2-4x+2,
设2x+1=t,∴x=
,
∴f(t)=(
)2-4×
+2=
t2-
t+
;
f(3-4x)=
(3-4x)2-
(3-4x)+
=4x2+4x-1.
故答案为:4x2+4x-1.
设2x+1=t,∴x=
| t-1 |
| 2 |
∴f(t)=(
| t-1 |
| 2 |
| t-1 |
| 2 |
| 1 |
| 4 |
| 5 |
| 2 |
| 17 |
| 4 |
f(3-4x)=
| 1 |
| 4 |
| 5 |
| 2 |
| 17 |
| 4 |
故答案为:4x2+4x-1.
点评:本题考查了用换元法求函数解析式的问题,解题的关键是求出f(t)的解析式,是基础题.

练习册系列答案
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
设向量
、
满足:|
|=2,|
|=1,
,
的夹角是60°,若2t
+7
与
+t
的夹角为钝角,则t的范围是( )
| e1 |
| e2 |
| e1 |
| e2 |
| e1 |
| e2 |
| e1 |
| e2 |
| e1 |
| e2 |
A、(-7,-
| ||||||||||
B、(-7,-
| ||||||||||
C、[-7,-
| ||||||||||
D、(-∞,-7)∪(-
|
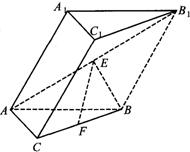 如图,在斜三棱柱ABC-A1B1C1中,侧面A1ABB1是菱形,且垂直于底面ABC,∠A1AB=60°,E,F分别是AB1,BC的中点.
如图,在斜三棱柱ABC-A1B1C1中,侧面A1ABB1是菱形,且垂直于底面ABC,∠A1AB=60°,E,F分别是AB1,BC的中点.