题目内容
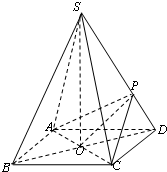 四棱锥S-ABCD的底面是边长为2的正方形,每条侧棱的长都是底面边长的
四棱锥S-ABCD的底面是边长为2的正方形,每条侧棱的长都是底面边长的| 2 |
(Ⅰ)当SP:PD为何值时,直线SD⊥平面PAC,
(Ⅱ)在(1)的条件下,侧棱SC上是否存在一点E,使得BE∥平面PAC,若存在,求SE:EC的值,若不存在,请说明理由.
考点:直线与平面垂直的判定,直线与平面平行的性质
专题:综合题,空间位置关系与距离
分析:(Ⅰ)根据已知可求得∠DPO=90°,由正方形边长2,则SD=2
,又OD=
,可求∠SDO=60°,由cos∠SDO=
,可解得PD的值,从而可求SP:PD的比值.
(Ⅱ)取SD中点为N,因为PD:SP=1:3,则PN=PD,过N作PC的平行线与SC的交点即为E.在△BDN中知BN∥PO,又由于NE∥PC,即可得到平面BEN∥平面PAC,使得BE∥平面PAC,进而求得SE:EC的值.
| 2 |
| 2 |
| PD |
| OD |
(Ⅱ)取SD中点为N,因为PD:SP=1:3,则PN=PD,过N作PC的平行线与SC的交点即为E.在△BDN中知BN∥PO,又由于NE∥PC,即可得到平面BEN∥平面PAC,使得BE∥平面PAC,进而求得SE:EC的值.
解答:
 解:(Ⅰ)∵直线SD⊥平面PAC,OP?平面PAC,
解:(Ⅰ)∵直线SD⊥平面PAC,OP?平面PAC,
∴直线SD⊥OP,故∠DPO=90°.
由正方形边长2,则SD=2
,
又OD=
,所以∠SDO=60°,
由cos∠SDO=
,可解得:PD=OD×cos∠SDO=
×
=
,
故SP:PD=(2
-
):
=3:1.
(Ⅱ)在棱SC上存在一点E,使BE∥平面PAC,由(Ⅱ)可得PD=
,
故可在SP上取一点N,使PN=PD,
过N作PC的平行线与SC的交点即为E,连结BN,
在△BDN中知BN∥PO,又由于NE∥PC,
故平面BEN∥平面PAC,得BE∥平面PAC,
由于SN:NP=2:1,故SE:EC=2:1.
 解:(Ⅰ)∵直线SD⊥平面PAC,OP?平面PAC,
解:(Ⅰ)∵直线SD⊥平面PAC,OP?平面PAC,∴直线SD⊥OP,故∠DPO=90°.
由正方形边长2,则SD=2
| 2 |
又OD=
| 2 |
由cos∠SDO=
| PD |
| OD |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
故SP:PD=(2
| 2 |
| ||
| 2 |
| ||
| 2 |
(Ⅱ)在棱SC上存在一点E,使BE∥平面PAC,由(Ⅱ)可得PD=
| ||
| 2 |
故可在SP上取一点N,使PN=PD,
过N作PC的平行线与SC的交点即为E,连结BN,
在△BDN中知BN∥PO,又由于NE∥PC,
故平面BEN∥平面PAC,得BE∥平面PAC,
由于SN:NP=2:1,故SE:EC=2:1.
点评:本题主要考查了立体几何中平面与平面平行的性质以及线段垂直平面的性质,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
数列{an}满足a1=
,
=
-1(n∈N*),则a10=( )
| 1 |
| 2 |
| 1 |
| an+1-1 |
| 1 |
| an-1 |
A、
| ||
B、
| ||
C、
| ||
D、
|
在直角梯形ABCD中,AB∥CD,∠ABC=90°,AB=2BC=2CD,则cos∠DAC=( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若(1-x)5=a0+a1(1+x)+a2(1+x)2+…+a5(1+x)5,则a1 十a2 十a3十a4十a5的值等于( )
| A、-31 | B、0 | C、1 | D、32 |
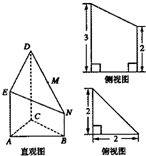 如图是某几何体的直观图与三视图的侧视图、俯视图.在直观图中,2BN=AE,M是ND的中点.侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
如图是某几何体的直观图与三视图的侧视图、俯视图.在直观图中,2BN=AE,M是ND的中点.侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.