题目内容
已知A,B是以O为圆心的单位圆上的动点,且|
|=
,则
•
=( )
| AB |
| 2 |
| OB |
| AB |
| A、-1 | ||||
| B、1 | ||||
C、-
| ||||
D、
|
考点:平面向量数量积的运算
专题:计算题,平面向量及应用
分析:运用勾股定理的逆定理,可得可得△OAB为等腰直角三角形,则
,
的夹角为45°,再由向量的数量积的定义计算即可得到.
| OB |
| AB |
解答:
解:由A,B是以O为圆心的单位圆上的动点,且|
|=
,
即有|
|2+|
|2=|
|2,
可得△OAB为等腰直角三角形,
则
,
的夹角为45°,
即有
•
=|
|•|
|•cos45°=1×
×
=1.
故选:B.
| AB |
| 2 |
即有|
| OA |
| OB |
| AB |
可得△OAB为等腰直角三角形,
则
| OB |
| AB |
即有
| OB |
| AB |
| OB |
| AB |
| 2 |
| ||
| 2 |
故选:B.
点评:本题考查向量的数量积的定义,运用勾股定理的逆定理得到向量的夹角是解题的关键.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
F是双曲线C:
-
=1(a>0,b>0)的右焦点,过点F向C的一条渐近线引垂线,垂足为 A,交另一条渐近线于点 B.若2
=
,则C的离心率是( )
| x2 |
| a2 |
| y2 |
| b2 |
| AF |
| FB |
A、
| ||||
| B、2 | ||||
C、
| ||||
D、
|
若向量
,
不共线,则下列各组向量中,可以作为一组基底的是( )
| a |
| b |
A、
| ||||||||||||
B、3
| ||||||||||||
C、
| ||||||||||||
D、2
|
甲乙两名同学参加某项技能比赛,7名裁判给两人打出的分数如下茎叶图所示,依此判断( )

| A、甲成绩稳定且平均成绩较高 |
| B、乙成绩稳定且平均成绩较高 |
| C、甲成绩稳定,乙平均成绩较高 |
| D、乙成绩稳定,甲平均成绩较高 |
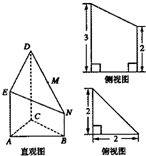 如图是某几何体的直观图与三视图的侧视图、俯视图.在直观图中,2BN=AE,M是ND的中点.侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.
如图是某几何体的直观图与三视图的侧视图、俯视图.在直观图中,2BN=AE,M是ND的中点.侧视图是直角梯形,俯视图是等腰直角三角形,有关数据如图所示.