题目内容

不定方程a+b+c+d+e+f=11的正整数解有多少组，非负整数解数有多少组．
考点：多元一次不定方程
专题：选作题,排列组合
分析：a+b+c+d+e+f=11的正整数解，转化为10个球中插入5个板，非负整数解数，转化为11+6-1个球中插入5个板．
解答： 解：a+b+c+d+e+f=11的正整数解，转化为10个球中插入5个板，故共有
C
5
10
=252组，
非负整数解数有
C
6-1
11+6-1
=4368组．
点评：将a1+a2+…+an=m的一组非负整数解一一对应m个相同的球和n-1个插板的一个摆法．
练习册系列答案
相关题目
已知点（1，
1
3
）是函数f（x）=ax（a＞0且a≠1）的图象上一点，等比数列{an}的前n项和为f（n）-c，数列{bn}（bn＞0）的首项为c，且前n项和Sn满足Sn-Sn-1=
Sn
+
Sn+1
（n≥2）．
（1）求数列{an}和{bn}的通项公式；
（2）若数列{
1
bnbn+1
}前n项和为Tn，问Tn＞
1000
2014
的最小正整数n是多少？
lim
n→∞
（1+
1
3
+
1
9
+…+
1
3n
）
等比数列{an}中，a1，a2，a3分别是下表一、二、三行中的某一个数，且a1，a2，a3中任何两个数不在下表同一列，且a1＜a2＜a3，
一列 二列 三列
第一行 2 3 12
第二行 4 6 14
第三行 8 9 18
（1）求数列{an}的通项公式；
（2）若数列{bn}满足bn=an+lnan，求数列{bn}前n项和．
已知函数f（x）=
1
2
x2+
1
2
x，数列{an}的前n项和为Sn，点（n，Sn）（n∈N*）均在函数y=f（x）的图象上．
（Ⅰ） 求数列{an}的通项公式an；
（Ⅱ）若bn=
an
2n
，求数列{bn}的前n项和Tn．
设命题p：函数y=ax在R上单调递增，命题q：不等式x2-ax+1＞0对一切x∈R恒成立，若“?p”为真，“p∨q”为真，求实数a的取值范围．
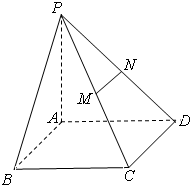如图，在四棱锥P-ABCD中，PA⊥平面ABCD，底面ABCD是矩形，M、N分别是PC、PD的中点．
（1）求证：MN∥平面PAB；
（2）若PA=2，AB=1，BC=
3
，求直线PC与平面ABCD所成的角．
如图是一个组合几何体的三视图，则该几何体的表面积是
 
已知α是第三象限角，sinα=-
1
3
，则
1
tanα
=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网