题目内容
正方形ABCD的边长为2,
=2
,
=
(
+
),则
•
= .
| DE |
| EC |
| DF |
| 1 |
| 2 |
| DC |
| DB |
| BE |
| DF |
考点:平面向量数量积的运算
专题:数形结合,平面向量及应用
分析:画出图形,利用正方形的边角关系以及题目中的条件,代入向量计算即可.
解答:
解:如图所示,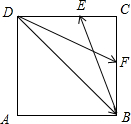
正方形ABCD中,边长为AB=2,
=2
,
=
(
+
),
∴
•
=(
+
)•
(
+
)
=
•
+
•
+
•
+
•
=
×2×2cos90°+
×
×2cos180°+
×2×2
cos135°+
×
×2
cos135°
=0-
-2-
=-
;
故答案为:-
.

正方形ABCD中,边长为AB=2,
| DE |
| EC |
| DF |
| 1 |
| 2 |
| DC |
| DB |
∴
| BE |
| DF |
| BC |
| CE |
| 1 |
| 2 |
| DC |
| DB |
=
| 1 |
| 2 |
| BC |
| DC |
| 1 |
| 2 |
| CE |
| DC |
| 1 |
| 2 |
| BC |
| DB |
| 1 |
| 2 |
| CE |
| DB |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
| 2 |
| 3 |
| 2 |
=0-
| 2 |
| 3 |
| 2 |
| 3 |
| 10 |
| 3 |
故答案为:-
| 10 |
| 3 |
点评:本题考查了平面向量的数量积的运算问题,也考查了数形结合的数学思想,是基础题目.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设集合M={x∈N|x2+x-6<0},P={x|(x-1)(x-3)≤0},则M∩P=( )
| A、[1,2) | B、[1,2] |
| C、{1,2} | D、{1} |