题目内容
10.已知向量$\overrightarrow{a}$=(-3,4),|$\overrightarrow{b}$|=10,且$\overrightarrow{a}$⊥$\overrightarrow{b}$,则$\overrightarrow{b}$的坐标是( )| A. | (-8,6) | B. | (8,-6) | C. | (-8,-6)或(8,6) | D. | (-8,6)或(8,-6) |
分析 设$\overrightarrow{b}$的坐标是(x,y),根据题意得到方程组,解得即可.
解答 解:设$\overrightarrow{b}$的坐标是(x,y),
∵向量$\overrightarrow{a}$=(-3,4),|$\overrightarrow{b}$|=10,且$\overrightarrow{a}$⊥$\overrightarrow{b}$,
∴$\left\{\begin{array}{l}{-3x+4y=0}\\{{x}^{2}+{y}^{2}=100}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=8}\\{y=6}\end{array}\right.$或$\left\{\begin{array}{l}{x=-8}\\{y=-6}\end{array}\right.$,
故$\overrightarrow{b}$的坐标是(8,6),或(-8,-6).
故选:C.
点评 本题考查了向量的坐标运算,向量的数量积运算和向量的模的计算,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.某产品的定价为x(元),总收益为y(元),已知y=-2x2+400x+8600,则有最大收益时,此产品的定价应为( )
| A. | 400元 | B. | 200元 | C. | 8600元 | D. | 100元 |
2.设A={x|$\frac{1}{x}$<0},S=R,则∁SA=( )
| A. | {x|$\frac{1}{x}$<0} | B. | {x|x<0} | C. | {x|x≤0} | D. | {x|x≥0} |
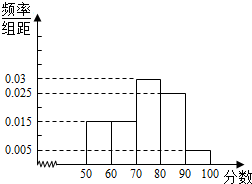 为更好地迎接江苏省学业水平测试,某校针对本届高二文科学生,进行了物理学科模拟测试,从参加测试的学生中抽出60名学生,对他们的物理成绩进行统计(注:学生成绩均为整数且满分为100分),并把其中成绩不低于50分的分成五段:[50,60),[60,70)…[90,100],画出如下部分频率分布直方图.请观察图形的相关信息,回答下列问题:
为更好地迎接江苏省学业水平测试,某校针对本届高二文科学生,进行了物理学科模拟测试,从参加测试的学生中抽出60名学生,对他们的物理成绩进行统计(注:学生成绩均为整数且满分为100分),并把其中成绩不低于50分的分成五段:[50,60),[60,70)…[90,100],画出如下部分频率分布直方图.请观察图形的相关信息,回答下列问题: