题目内容
8．已知abc＞0，则在下列各选项中，二次函数f（x）=ax2+bx+c的图象不可能是（ ）| A． |  | B． |  | C． |  | D． |  |
分析 根据二次函数的性质分别对各个选项进行判断即可．
解答 解：对于A：a＜0，c＜0，
若abc＞0，则b＞0，
显然-$\frac{b}{2a}$＞0，得到b＞0，符合题意；
对于B：a＞0，c＜0，
若abc＞0，则b＜0，
而对称轴x=-$\frac{b}{2a}$＞0，得：b＜0，符合题意；
对于C：a＜0，c＞0，
若abc＞0，则b＜0，
而对称轴x=-$\frac{b}{2a}$＜0，得：b＜0，符合题意；
对于D：a＞0，c＜0，
若abc＞0，则b＜0，
而对称轴x=-$\frac{b}{2a}$＜0，得：b＞0，不符合题意；
故选：D．
点评 本题考查了二次函数的性质，考查数形结合思想，是一道基础题．
练习册系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
19．已知f（x）=sin$\frac{π}{3}$x，A={1，2，3，4，5，6，7，8}现从集合A中任取两个不同元素s、t，则使得f（s）•f（t）=0的可能情况为 （ ）
| A． | 12种 | B． | 13种 | C． | 14种 | D． | 15种 |
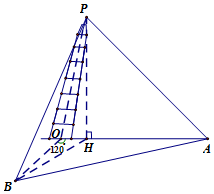上海市松江区天马山上的“护珠塔”因其倾斜度超过意大利的比萨斜塔而号称“世界第一斜塔”．兴趣小组同学实施如下方案来测量塔的倾斜度和塔高：如图，记O点为塔基、P点为塔尖、点P在地面上的射影为点H．在塔身OP射影所在直线上选点A，使仰角k∠HAP=45°，过O点与OA成120°的地面上选B点，使仰角∠HPB=45°（点A、B、O都在同一水平面上），此时测得∠OAB=27°，A与B之间距离为33.6米．试求：
3．方程4x-4•2x-5=0的解是（ ）
| A． | x=0或x=log25 | B． | x=-1或x=5 | C． | x=log25 | D． | x=0 |
17．集合P={x|x＜2}，集合Q={y|y＜1}，则P与Q的关系为（ ）
| A． | P⊆Q | B． | Q⊆P | C． | P=Q | D． | 以上都不正确 |
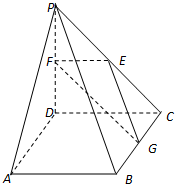如图，在四棱锥P-ABCD中，ABCD是正方形，PD⊥平面ABCD，PD=AB=2，E，F，G分别是PC，PD，BC的中点．