��Ŀ����
16��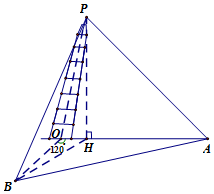 �Ϻ����ɽ�������ɽ�ϵġ���������������б�ȳ���������ı���б�����ųơ������һб��������ȤС��ͬѧʵʩ���·���������������б�Ⱥ����ߣ���ͼ����O��Ϊ������P��Ϊ���⡢��P�ڵ����ϵ���ӰΪ��H��������OP��Ӱ����ֱ����ѡ��A��ʹ����k��HAP=45�㣬��O����OA��120��ĵ�����ѡB�㣬ʹ���ǡ�HPB=45�㣨��A��B��O����ͬһˮƽ���ϣ�����ʱ��á�OAB=27�㣬A��B֮�����Ϊ33.6�ף�����
�Ϻ����ɽ�������ɽ�ϵġ���������������б�ȳ���������ı���б�����ųơ������һб��������ȤС��ͬѧʵʩ���·���������������б�Ⱥ����ߣ���ͼ����O��Ϊ������P��Ϊ���⡢��P�ڵ����ϵ���ӰΪ��H��������OP��Ӱ����ֱ����ѡ��A��ʹ����k��HAP=45�㣬��O����OA��120��ĵ�����ѡB�㣬ʹ���ǡ�HPB=45�㣨��A��B��O����ͬһˮƽ���ϣ�����ʱ��á�OAB=27�㣬A��B֮�����Ϊ33.6�ף�������1�����ߣ����߶�PH�ij�����ȷ��0.1�ף���
��2����������б�ȣ���PO��PH�ļнǣ���ȷ��0.1�㣩��
���� ��1���������֪����PAH����PBH��Ϊ����ֱ�������Σ�AH=BH=x����HAB=27�㣬AB=33.6���������x=$\frac{\frac{AB}{2}}{cos��HAB}$=$\frac{16.8}{cos27��}$=18.86��
��2����OBH=180��-120��-2��27��=6�㣬BH=18.86�������Ҷ�����֪��$\frac{OH}{sin��OBH}$=$\frac{BH}{sin��BOH}$��OH=$\frac{18.86��sin6��}{sin120��}$=2.28������б�ǡ�OPH=arctan$\frac{OH}{PH}$=arctan$\frac{2.28}{18.86}$=6.89�㣮
��� �⣺��1��������PH=x��������֪����HAP=45�㣬��HBP=45�㣬
���PAH����PBH��Ϊ����ֱ�������Σ�
��AH=BH=x����2�֣�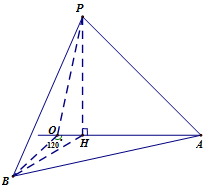
�ڡ�AHB�У�AH=BH=x����HAB=27�㣬AB=33.6��
��x=$\frac{\frac{AB}{2}}{cos��HAB}$=$\frac{16.8}{cos27��}$=18.86����6�֣�
��2���ڡ�BOH�У���BOH=120�㣬
���OBH=180��-120��-2��27��=6�㣬BH=18.9��
��$\frac{OH}{sin��OBH}$=$\frac{BH}{sin��BOH}$��
��OH=$\frac{18.86��sin6��}{sin120��}$=2.28������10�֣�
���OPH=arctan$\frac{OH}{PH}$=arctan$\frac{2.28}{18.86}$��6.9�㣬����13�֣�
������18.9�ף�������б��Ϊ6.9�㣮 ����14�֣�
���� ���⿼��������ε��ۺ�Ӧ�ã��������Ҷ����������Ǻ�����Ӧ�ã��������ν��˼�룬�����е��⣮

| A�� | $y=\left\{{\begin{array}{l}{2-x��x��1}\\{x��x��1}\end{array}}\right.$ | B�� | $y=\left\{{\begin{array}{l}{2-x��x��1}\\{x��x��1}\end{array}}\right.$ | C�� | $y=\left\{{\begin{array}{l}{x��x��1}\\{2-x��x��1}\end{array}}\right.$ | D�� | $y=\left\{{\begin{array}{l}{2-x��x��1}\\{x��x��1}\end{array}}\right.$ |
| A�� | $4\sqrt{3}��$ | B�� | $\frac{16��}{3}$ | C�� | 16�� | D�� | $\frac{32��}{3}$ |



