题目内容
18.数列{an}是首项为1,公差为2的等差数列,Sn是它前n项和,则$\lim_{n→∞}\frac{S_n}{a_n^2}$=$\frac{1}{4}$.分析 求出数列的和以及通项公式,然后求解数列的极限即可.
解答 解:数列{an}是首项为1,公差为2的等差数列,Sn=$n+\frac{n(n-1)×2}{2}$=n2.an=1+(n-1)×2=2n-1,
则$\lim_{n→∞}\frac{S_n}{a_n^2}$=$\underset{lim}{n→∞}$$\frac{{n}^{2}}{(2n-1)^{2}}$=$\frac{1}{4}$
故答案为:$\frac{1}{4}$;
点评 本题考查等差数列求和,数列的极限的求法,考查计算能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.已知函数f(x)=x5+2x4+x3-x2+3x-5,用秦九韶算法计算,当x=5时,V3=( )
| A. | 27 | B. | 36 | C. | 54 | D. | 179 |
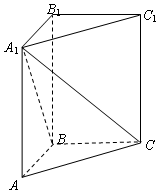 在正三棱柱ABC-A1B1C1中,AB=1,BB1=2,求:
在正三棱柱ABC-A1B1C1中,AB=1,BB1=2,求: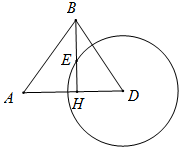 如图,我海监船在D岛海域例行维权巡航,某时刻航行至A处,此时测得其北偏东30°方向与它相距20海里的B处有一外国船只,且D岛位于海监船正东18海里处.
如图,我海监船在D岛海域例行维权巡航,某时刻航行至A处,此时测得其北偏东30°方向与它相距20海里的B处有一外国船只,且D岛位于海监船正东18海里处.


