题目内容
3.方程4x-4•2x-5=0的解是( )| A. | x=0或x=log25 | B. | x=-1或x=5 | C. | x=log25 | D. | x=0 |
分析 设2x=t,t>0,则原方程等价转化为:t2-4t-5=0,由此能求出结果.
解答 解:∵4x-4•2x-5=0,
∴设2x=t,t>0,
则原方程等价转化为:t2-4t-5=0,
解得t=5,或f=-1(舍),
∴2x=5,解得x=log25.
故选:C.
点评 本题考查方程的解的求法,是基础题,解题时要认真审题,注意换元法的合理运用.

练习册系列答案
相关题目
12.设变量x,y满足约束条件$\left\{\begin{array}{l}{y≥x}\\{x+2y≤2}\\{x≥-2}\end{array}\right.$,则z=x-3y的最大值为( )
| A. | -2 | B. | 4 | C. | -6 | D. | -8 |
7.若x轴为曲线f(x)=x3-ax-$\frac{1}{4}$的切线,则a=( )
| A. | $\frac{3}{4}$ | B. | $-\frac{3}{4}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
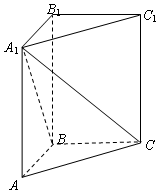 在正三棱柱ABC-A1B1C1中,AB=1,BB1=2,求:
在正三棱柱ABC-A1B1C1中,AB=1,BB1=2,求:



