题目内容
12.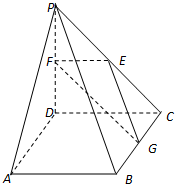 如图,在四棱锥P-ABCD中,ABCD是正方形,PD⊥平面ABCD,PD=AB=2,E,F,G分别是PC,PD,BC的中点.
如图,在四棱锥P-ABCD中,ABCD是正方形,PD⊥平面ABCD,PD=AB=2,E,F,G分别是PC,PD,BC的中点.(1)求证:平面PAB∥平面EFG;
(2)证明:平面EFG⊥平面PAD;
(3)在线段PB上确定一点Q,使PC⊥平面ADQ,并给出证明.
分析 (1)运用面面平行的判定定理,先证线面平行,即可得到证明;
(2)由线面垂直的性质和面面垂直的判定定理,即可得证;
(3)Q为线段PB中点时,PC⊥平面ADQ.运用线面垂直的判定定理即可得到结论.
解答  证明:(1)E,F分别是线段PC,PD的中点,所以EF∥CD,
证明:(1)E,F分别是线段PC,PD的中点,所以EF∥CD,
又ABCD为正方形,AB∥CD,
所以EF∥AB,
又EF?平面PAB,所以EF∥平面PAB.
因为E,G分别是线段PC,BC的中点,所以EG∥PB,
又EG?平面PAB,所以,EG∥平面PAB.
所以平面EFG∥平面PAB;
(2)因为CD⊥AD,CD⊥PD,AD∩PD=D,所以CD⊥平面PAD,
又EF∥CD,所以EF⊥平面PAD,所以平面EFG⊥平面PAD;
(3)Q为线段PB中点时,PC⊥平面ADQ.
取PB中点Q,连接DE,EQ,AQ,
由于EQ∥BC∥AD,所以ADEQ为平面四边形,
由PD⊥平面ABCD,得AD⊥PD,
又AD⊥CD,PD∩CD=D,所以AD⊥平面PDC,
所以AD⊥PC,
又三角形PDC为等腰直角三角形,E为斜边中点,所以DE⊥PC,
AD∩DE=D,所以PC⊥平面ADQ.
点评 本题考查线面位置关系的证明,主要是面面平行和面面垂直、以及线面垂直的证明,注意运用转化思想,考查推理能力,属于中档题.

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案 期末好成绩系列答案
期末好成绩系列答案
相关题目
9.设集合M={x|-3<x<2},N={x|1≤x≤3},则M∩N=( )
| A. | [2,3] | B. | [1,2] | C. | (2,3] | D. | [1,2) |
7.若x轴为曲线f(x)=x3-ax-$\frac{1}{4}$的切线,则a=( )
| A. | $\frac{3}{4}$ | B. | $-\frac{3}{4}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
1.已知函数$f(x)=\left\{\begin{array}{l}|lg(-x)|,x<0\\{x^3}-6x+4,x≥0\end{array}\right.$若关于x的函数y=[f(x)]2-bf(x)+1有8个不同的零点,则实数b的取值范围为( )
| A. | (2,8) | B. | $[2,\frac{17}{4})$ | C. | $(2,\frac{17}{4}]$ | D. | (2,8] |
2.已知f(x)=x3+3ax2+bx+a2在x=-1时有极值0,则a-b=( )
| A. | -7 | B. | -2 | C. | -7和-2 | D. | 以上答案都不对 |



