题目内容
过点P（2，3）的直线l与圆x2+y2=25相交于A，B两点，当弦AB最短时，直线l的方程式是（ ）
| A、2x+3y-13=0 |
| B、2x-3y+5=0 |
| C、3x-2y=0 |
| D、3x+2y-12=0 |
考点：直线和圆的方程的应用
专题：计算题,直线与圆
分析：由题意得，点P在圆的内部，故当弦AB和点P与圆心的连线垂直时，弦AB最短，由垂直的条件求出弦的斜率，由点斜式求得弦AB所在的直线的方程，再化为一般式．
解答：
解：因为点P（2，3）到圆心（0，0）的距离等于
，小于半径5，
故此点在圆x2+y2=25的内部，
故当弦AB和点P与圆心（0，0）的连线垂直时，弦AB最短．
弦AB的斜率为
=-
，由点斜式求得弦AB所在的直线的方程为
y-3=-
（x-2），即2x+3y-13=0，
故选A．
| 13 |
故此点在圆x2+y2=25的内部，
故当弦AB和点P与圆心（0，0）的连线垂直时，弦AB最短．
弦AB的斜率为
| -1 | ||
|
| 2 |
| 3 |
y-3=-
| 2 |
| 3 |
故选A．
点评：本题考查点与圆的位置关系的判断，以及用点斜式求直线的方程．
练习册系列答案
相关题目
已知tanα=2，则
的值为（ ）
| cos(π+2α) | ||
cos(
|
A、-
| ||
| B、1 | ||
C、
| ||
D、-
|
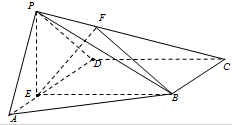如图，在四棱锥P-ABCD中，E为AD上一点，PE⊥平面ABCD，AD∥BC，AD⊥CD，BC=ED=2AE=2，EB=3，F为PC上一点，且CF=2FP．
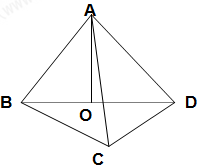设A在平面BCD内的射影是直角三角形BCD的斜边BD的中点O，AC=BC=1，CD=