题目内容
已知tan（θ+
）=3，则sin2θ-2cos2θ= ．
| π |
| 4 |
考点：两角和与差的正切函数,二倍角的余弦
专题：三角函数的求值
分析：利用两角差的正切可求得tanθ=tan[（θ+
）-
]=
，再将所求的关系式转化为sin2θ-2cos2θ=
=
，计算即可．
| π |
| 4 |
| π |
| 4 |
| 1 |
| 2 |
| 2sinθcosθ-2cos2θ |
| sin2θ+cos2θ |
| 2tanθ-2 |
| tan2θ+1 |
解答：
解：∵tan（θ+
）=3，
∴tanθ=tan[（θ+
）-
]=
=
=
，
∴sin2θ-2cos2θ=
=
=
=-
．
故答案为：-
．
| π |
| 4 |
∴tanθ=tan[（θ+
| π |
| 4 |
| π |
| 4 |
tan(θ+
| ||||
1+tan(θ+
|
| 3-1 |
| 1+3 |
| 1 |
| 2 |
∴sin2θ-2cos2θ=
| 2sinθcosθ-2cos2θ |
| sin2θ+cos2θ |
| 2tanθ-2 |
| tan2θ+1 |
| 1-2 | ||
|
| 4 |
| 5 |
故答案为：-
| 4 |
| 5 |
点评：本题考查两角和与差的正切，考查二倍角的余弦与正弦，“弦”化“切”是关键，考查转化思想．
练习册系列答案
阅读快车系列答案
相关题目
过点P（2，3）的直线l与圆x2+y2=25相交于A，B两点，当弦AB最短时，直线l的方程式是（ ）
| A、2x+3y-13=0 |
| B、2x-3y+5=0 |
| C、3x-2y=0 |
| D、3x+2y-12=0 |
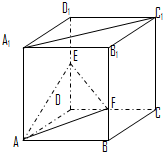如图，在棱长为1的正方体ABCD-A1B1C1D1中，点E是棱D1D的中点，点F在棱B1B上且B1F=2FB．
如图在△ABC中，AB=2，AC=3，D为BC的中点，则向量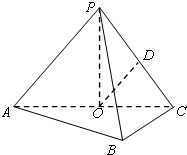
如图，在三棱锥P-ABC中，AB⊥BC，AB=BC=
如图①，有一个长方形状的敞口玻璃容器，底面是边长为20cm的正方形，高为30cm，内有20cm深的溶液，现将此容器倾斜一定角度α（图②），且倾斜时底面的一条棱始终在桌面上（图①，②均为容器的纵截面）．若a=9，b=12，A=45°，则△ABC有（ ）
| A、一解 | B、两解 |
| C、无解 | D、不能确定 |