题目内容
我们知道:对于任意n∈N*有(1+2+3+…+n)2=13+23+…+n3成立,尝试将此真命题进行推广:若数列{an}对于任意n∈N*有(a1+a2+a3+…+an)2=a13+a23+…+an3则称数列{an}具有”D性质”
(1)若由三项非零数组成的数列a1,a2,a3具有”D性质”,求出所有满足条件的数列{an};
(2)若数列{bn}b1=1,且Sn=
(n∈N*),则该数列具有”D性质”么?说明理由(Sn为数列前n项和);
(3)若数列{cn}c1=1,c2=2满足cn+12-cn+1=2Sn,(n∈N*)判断并证明该数列是否具有”D性质”.(Sn为数列前n项和)
(1)若由三项非零数组成的数列a1,a2,a3具有”D性质”,求出所有满足条件的数列{an};
(2)若数列{bn}b1=1,且Sn=
| (n+1)bn |
| 2 |
(3)若数列{cn}c1=1,c2=2满足cn+12-cn+1=2Sn,(n∈N*)判断并证明该数列是否具有”D性质”.(Sn为数列前n项和)
考点:数学归纳法
专题:计算题,等差数列与等比数列,点列、递归数列与数学归纳法
分析:(1)求出n=1,2,3对应的a1,a2,a3的值即可;
(2)将n换成n-1,相减,运用新定义,即可得证;
(3){cn}具有”D性质”,运用数学归纳法证明即可.
(2)将n换成n-1,相减,运用新定义,即可得证;
(3){cn}具有”D性质”,运用数学归纳法证明即可.
解答:
解:(1)当n=1时
=
⇒a1=1;
当n=2时(
+
)2=
+
⇒a2=-1或2,
当n=3时(
+
+a3)2=
+
+
⇒
;
∴所有满足条件的数列{an}:a1=1,a2=-1,a3=1
或a1=1,a2=2,a3=-2或a1=1,a2=2,a3=3;
(2)Sn=
,Sn-1=
(n∈N*,n>1)⇒(n-1)bn=nbn-1
则
-
=0,即{
}为等差数列,且bn=n,则该数列具有”D性质”;
(3){cn}具有”D性质”.运用数学归纳法证明如下:
1)当n=1时c12=
,”D性质成立”;
2)假设当n=k(k∈N*)时有(c1+…+ck)2=c13+c23+…+ck3成立.
则当n=k+1时有(c1+…+ck+1)2=(Sk+ck+1)2=
+2ck+1Sk+
=c13+c23+…+ck3+(ck+12-ck+1)ck+1+
=c13+c23+…+ck3+
∴{cn}具有”D性质”.
| a | 2 1 |
| a | 3 1 |
当n=2时(
| a | 1 |
| a | 2 |
| a | 3 1 |
| a | 3 2 |
当n=3时(
| a | 1 |
| a | 2 |
| a | 3 1 |
| a | 3 2 |
| a | 3 3 |
|
|
|
∴所有满足条件的数列{an}:a1=1,a2=-1,a3=1
或a1=1,a2=2,a3=-2或a1=1,a2=2,a3=3;
(2)Sn=
| (n+1)bn |
| 2 |
| (n)bn-1 |
| 2 |
则
| bn |
| n |
| bn-1 |
| n-1 |
| bn |
| n |
(3){cn}具有”D性质”.运用数学归纳法证明如下:
1)当n=1时c12=
| c | 3 1 |
2)假设当n=k(k∈N*)时有(c1+…+ck)2=c13+c23+…+ck3成立.
则当n=k+1时有(c1+…+ck+1)2=(Sk+ck+1)2=
| S | 2 k |
| c | 2 k+1 |
=c13+c23+…+ck3+(ck+12-ck+1)ck+1+
| c | 2 k+1 |
| c | 3 k+1 |
∴{cn}具有”D性质”.
点评:本题新定义的理解和运用,考查等差数列的通项公式,以及数学归纳法的证明,考查运算能力,属于中档题.

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
已知A={x|y=lo
},集合B={y|y=
,x>3},则A∩B=( )
| g | (x+1) 2 |
| 1 |
| x |
A、(
| ||
B、(0,
| ||
| C、(-1,+∞) | ||
D、(-1,
|
下列命题为“p或q”的形式的是( )
A、
| ||
| B、2是4和6的公约数 | ||
| C、Φ≠{0} | ||
| D、2≤3 |
过点P(2,3)的直线l与圆x2+y2=25相交于A,B两点,当弦AB最短时,直线l的方程式是( )
| A、2x+3y-13=0 |
| B、2x-3y+5=0 |
| C、3x-2y=0 |
| D、3x+2y-12=0 |
 如图,四棱柱A1B1C1D1-ABCD中,底面ABCD为直角梯形,AB∥CD,∠ABC=90°,BC1=B1C,
如图,四棱柱A1B1C1D1-ABCD中,底面ABCD为直角梯形,AB∥CD,∠ABC=90°,BC1=B1C,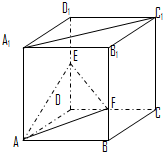 如图,在棱长为1的正方体ABCD-A1B1C1D1中,点E是棱D1D的中点,点F在棱B1B上且B1F=2FB.
如图,在棱长为1的正方体ABCD-A1B1C1D1中,点E是棱D1D的中点,点F在棱B1B上且B1F=2FB. 如图①,有一个长方形状的敞口玻璃容器,底面是边长为20cm的正方形,高为30cm,内有20cm深的溶液,现将此容器倾斜一定角度α(图②),且倾斜时底面的一条棱始终在桌面上(图①,②均为容器的纵截面).
如图①,有一个长方形状的敞口玻璃容器,底面是边长为20cm的正方形,高为30cm,内有20cm深的溶液,现将此容器倾斜一定角度α(图②),且倾斜时底面的一条棱始终在桌面上(图①,②均为容器的纵截面).