题目内容
15.在10件产品中,有8种合格品,2件次品,从这10件产品中任意抽出3件,抽出的3件中至少有1件是次品的抽法种数为( )| A. | 64 | B. | 72 | C. | 384 | D. | 432 |
分析 间接法:任抽三件,再排除全是正品的,即可得到抽出的3件中至少有1件是次品的抽法
直接法,分两类一件次品和两件次品,根据分类计数原理可得.
解答 解:间接法:抽出的3件产品中至少有1件是次品的抽法有C103-C83=120-56=64种,
直接法,分两类一件次品和两件次品,故有C21C82+C22C81=56+8=64种,
故选:A
点评 本题考查组合知识的运用,考查学生利益数学知识解决实际问题的能力,属于基础题

练习册系列答案
相关题目
5.$(x+\frac{1}{x}){(ax-1)^5}$的展开式中各项系数的和为2,则该展开式中常数项为( )
| A. | -20 | B. | -10 | C. | 10 | D. | 20 |
3.为了解某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下列表:
已知在全部50人中随机抽取1人,抽到喜爱打篮球的学生的概率为$\frac{3}{5}$.
(1)请将上表补充完整(不用写计算过程);
(2)能否在犯错误的概率不超过0.005的前提下认为喜爱打篮球与性别有关?说明你的理由;下面的临界值表供参考:
(参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d)
| 喜爱打篮球 | 不喜爱打篮球 | 合计 | |
| 男生 | 20 | 5 | 25 |
| 女生 | 10 | 15 | 25 |
| 合计 | 30 | 20 | 50 |
(1)请将上表补充完整(不用写计算过程);
(2)能否在犯错误的概率不超过0.005的前提下认为喜爱打篮球与性别有关?说明你的理由;下面的临界值表供参考:
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
20.已知函数$y=|{sin({2x-\frac{π}{6}})}|$,以下说法正确的是( )
| A. | 函数的最小正周期为$\frac{π}{4}$ | B. | 函数是偶函数 | ||
| C. | 函数图象的一条对称轴为$x=\frac{π}{3}$ | D. | 函数在$[{\frac{2π}{3},\frac{5π}{6}}]$上为减函数 |
7.已知数列{an}中,a1=3,an+1=$\frac{1}{{a}_{n}-1}$+1,则a2014=( )
| A. | -$\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | 3 | D. | 4 |
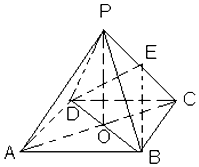 如图,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,E是PC的中点.求证:
如图,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,E是PC的中点.求证: