题目内容
20.已知函数$y=|{sin({2x-\frac{π}{6}})}|$,以下说法正确的是( )| A. | 函数的最小正周期为$\frac{π}{4}$ | B. | 函数是偶函数 | ||
| C. | 函数图象的一条对称轴为$x=\frac{π}{3}$ | D. | 函数在$[{\frac{2π}{3},\frac{5π}{6}}]$上为减函数 |
分析 根据正弦函数的图象及性质判断即可.
解答 解:由y=sin(2x-$\frac{π}{6}$)的图象关于x轴翻折下部分可得函数$y=|{sin({2x-\frac{π}{6}})}|$的图象,图象没有关于y轴对称,B不对.周期T=$\frac{π}{2}$,A不对,
对称轴方程$\frac{1}{2}kπ$+$\frac{π}{3}$,k=0时,可得C选择正确.
通过图象可得D不对.,
故选C
点评 本题主要考查三角函数的图象翻折问题和性质的运用,属于中档题.

练习册系列答案
相关题目
10.一个几何体的三视图及尺寸如图所示,则该几何体的体积为( )


| A. | 24 | B. | 30 | C. | 48 | D. | 72 |
11.已知$\overrightarrow a,\overrightarrow b$均为单位向量,它们的夹角为60°,那么$|{3\overrightarrow a+\overrightarrow b}|$等于( )
| A. | 4 | B. | $\sqrt{13}$ | C. | $\sqrt{10}$ | D. | $\sqrt{7}$ |
15.在10件产品中,有8种合格品,2件次品,从这10件产品中任意抽出3件,抽出的3件中至少有1件是次品的抽法种数为( )
| A. | 64 | B. | 72 | C. | 384 | D. | 432 |
12.某中学一位高三班主任对本班50名学生学习积极性和对待班级工作的态度进行调查,得到的统计数据如表所示:
(1)若不积极参加班级工作且学习积极性高的7名学生中有两名男生,现从中抽取两名学生参加某项活动,问两名学生中有1名男生的概率是多少?
(2)有多少的把握认为“学生的学习积极性与对待班级工作的态度”有关系?请说明理由.
附:
K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$.
| 积极参加班级工作 | 不积极参加班级工作 | 合计 | |
| 学习积极性高 | 18 | 7 | 25 |
| 学习积极性不高 | 6 | 19 | 25 |
| 合计 | 24 | 26 | 50 |
(2)有多少的把握认为“学生的学习积极性与对待班级工作的态度”有关系?请说明理由.
附:
| P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
10.已知△ABC的三个内角A,B,C满足2017cos2C-cos2A=2016-2sin2B,则$\frac{tanC•(tanA+tanB)}{tanA•tanB}$=( )
| A. | $\frac{2017}{2}$ | B. | $\frac{2}{2017}$ | C. | $\frac{1}{2016}$ | D. | $\frac{1}{1008}$ |
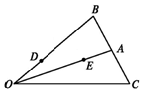 已知△OBC中,点A是线段BC的中点,点D是线段OB的一个靠近O的三等分点,设$\overrightarrow{OB}$=$\overrightarrow{a}$,$\overrightarrow{OC}$=$\overrightarrow{b}$
已知△OBC中,点A是线段BC的中点,点D是线段OB的一个靠近O的三等分点,设$\overrightarrow{OB}$=$\overrightarrow{a}$,$\overrightarrow{OC}$=$\overrightarrow{b}$