题目内容
10.已知数列{an}{满足a1=1,an+1-an=2,等比数列{bn}满足b1=a1,b4=8(I)求数列{an},{bn}的通项公式;
(II)设cn=an•bn,求数列{cn}的前n项和Sn.
分析 (I)利用等差数列与等比数列的通项公式即可得出.
(II)利用错位相减法、等比数列的求和公式即可得出.
解答 解:(I)由题意可知:an+1-an=2
∴数列{an}是以a1=1为首项,以d=2为公差的等差数列,…(1分)
∴数列{an}的通项公式an=2n-1,…(2分)
由等比数列{bn},${b_4}={b_1}•{q^3}$,而b1=a1,b4=8
∴q3=8,∴q=2
∴数列{bn}的通项公式${b_n}={2^{n-1}}$;…(5分)
(II)由(I)得an=2n-1,${b_n}={2^{n-1}}$,∴${c_n}=(2n-1)•{2^{n-1}}$,
∴Sn=c1+c2+…+cn=20+3•21+…+(2n-1)•2n-1①
∴$2{S_n}={2^1}+3•{2^2}+…+(2n-1)•{2^n}$②
由①-②得:∴$-{S_n}={2^0}+2•{2^1}+…+2•{2^{n-1}}-(2n-1)•{2^n}$
=$1+2[\frac{{{2^1}(1-{2^{n-1}})}}{1-2}]-(2n-1)•{2^n}$=-3+(2-2n)•2n.
∴${S_n}=3+(n-1)•{2^{n+1}}$…(10分)
点评 本题考查了错位相减法、等差数列与等比数列的通项公式与求和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
18.已知角α的终边过点$P(\frac{1}{2},\frac{{\sqrt{3}}}{2})$,则sinα=( )
| A. | $\frac{1}{2}$ | B. | $\sqrt{3}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $-\frac{{\sqrt{3}}}{2}$ |
5.如果直线 l 经过两直线2x-3y+1=0和3x-y-2=0的交点,且与直线y=x垂直,则原点到直线 l 的距离是( )
| A. | 2 | B. | 1 | C. | $\sqrt{2}$ | D. | 2$\sqrt{2}$ |
15.在10件产品中,有8种合格品,2件次品,从这10件产品中任意抽出3件,抽出的3件中至少有1件是次品的抽法种数为( )
| A. | 64 | B. | 72 | C. | 384 | D. | 432 |
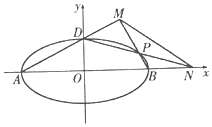 椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{3}}{2}$,a+b=3.
椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率e=$\frac{\sqrt{3}}{2}$,a+b=3.