题目内容
5．已知正四棱锥的底面边长是2cm，侧棱长是$\sqrt{3}$cm，则该正四棱锥的体积为$\frac{4}{3}c{m}^{3}$．分析 正四棱锥P-ABCD中，AB=2，PA=$\sqrt{3}$，设正四棱锥的高为PO，连结AO，求出PO，由此能求出该正四棱锥的体积．
解答 解：如图，正四棱锥P-ABCD中，AB=2cm，PA=$\sqrt{3}$cm，
设正四棱锥的高为PO，连结AO，
则AO=$\frac{1}{2}$AC=$\sqrt{2}$（cm）．
在直角三角形POA中，PO=$\sqrt{P{A}^{2}-A{O}^{2}}$=$\sqrt{3-2}$=1（cm）．
所以VP-ABCD=$\frac{1}{3}$•SABCD•PO=$\frac{1}{3}$×4×1=$\frac{4}{3}$（cm3）．
故答案为：$\frac{4}{3}$cm3
点评 本题考查正四棱锥的体积的求法，考查数据处理能力、运算求解能力以及应用意识，考查数形结合思想等，是中档题．
练习册系列答案
寒假学与练系列答案
相关题目
15．在10件产品中，有8种合格品，2件次品，从这10件产品中任意抽出3件，抽出的3件中至少有1件是次品的抽法种数为（ ）
| A． | 64 | B． | 72 | C． | 384 | D． | 432 |
16．若函数f（x）=$\frac{1}{3}{x^3}+a{x^2}$+bx+c有极值点x1，x2（x1＜x2），且f（x1）=x1，则关于x的方程[f（x）]2+2af（x）+b=0的不同实数根的个数为（ ）
| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
13．下列不等式中，正确的是（ ）
| A． | $tan\frac{13π}{4}＞tan\frac{13π}{3}$ | B． | $sin\frac{π}{5}＞cos\frac{π}{5}$ | C． | $cos\frac{3π}{5}＜cos（-\frac{2π}{5}）$ | D． | cos 55°＞tan 35° |
10．已知△ABC的三个内角A，B，C满足2017cos2C-cos2A=2016-2sin2B，则$\frac{tanC•（tanA+tanB）}{tanA•tanB}$=（ ）
| A． | $\frac{2017}{2}$ | B． | $\frac{2}{2017}$ | C． | $\frac{1}{2016}$ | D． | $\frac{1}{1008}$ |
14．圆心在x轴上，半径长为 $\sqrt{2}$，且过点（-2，1）的圆的方程为（ ）
| A． | （x+1）2+y2=2 | B． | x2+（y+2）2=2 | ||
| C． | （x+3）2+y2=2 | D． | （x+1）2+y2=2或（x+3）2+y2=2 |
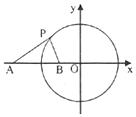已知圆C：x2+y2=9，点A（-5，0），直线l：x-2y=0．