题目内容
7．设复数z=a-i，其中i为虚数单位，a∈R．（1）若z2=-2i，求实数a的值；
（2）若a=2，求复平面内与$\frac{z}{1+i}$对应的点的坐标．
分析 （1）由z2=-2i，展开后利用复数相等的条件求得a值；
（2）利用复数代数形式的乘除运算化简即可求得复平面内与$\frac{z}{1+i}$对应的点的坐标．
解答 解：（1）∵z2=（a-i）2=a2-1-2ai，
由题意，a2-1-2ai=-2i，
∴$\left\{{\begin{array}{l}{{a^2}-1=0}\\{-2a=-2}\end{array}}\right.$，解得a=1．
（2）由题意，z=2-i，
∴$\frac{z}{1+i}=\frac{2-i}{1+i}=\frac{（2-i）（1-i）}{（1+i）（1-i）}=\frac{1-3i}{2}=\frac{1}{2}-\frac{3}{2}i$，
∴复数$\frac{z}{1+i}$在复平面内所对应的点坐标为$（\frac{1}{2}，-\frac{3}{2}）$．
点评 本题考查复数代数形式的乘除运算，考查复数相等的条件，是基础题．
练习册系列答案
相关题目
18．已知椭圆的长轴长是焦距的2倍，则椭圆的离心率为（ ）
| A． | 2 | B． | $\frac{{\sqrt{3}}}{3}$ | C． | $\frac{{\sqrt{2}}}{2}$ | D． | $\frac{1}{2}$ |
已知${a_n}=2n（n∈{N^*}）$，把数列{an}的各项按如图的规律排成一个三角形数阵，记F（p，q）表示第p行从左至右的第q个数，则F（8，6）的值为110．
12．若将函数f（x）=$\frac{1}{2}$sin（2x+$\frac{π}{3}$）图象上的每一个点都向左平移$\frac{π}{3}$个单位，得到g（x）的图象，则函数g（x）的单调递增区间为（ ）
| A． | [kπ-$\frac{π}{4}$，kπ+$\frac{π}{4}$]（k∈Z） | B． | [kπ+$\frac{π}{4}$，kπ+$\frac{3π}{4}$]（k∈Z） | ||
| C． | [kπ-$\frac{2π}{3}$，kπ-$\frac{π}{6}$]（k∈Z） | D． | [kπ-$\frac{π}{12}$，kπ+$\frac{5π}{12}$]（k∈Z） |
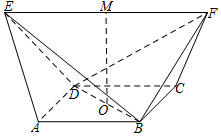如图，在五面体ABCDEF中，底面ABCD是正方形，△ADE，△BCF都是等边三角形，EF∥AB，且EF＞AB，M，O分别为EF，BD的中点，连接MO．