题目内容
设Sn表示数列{an}的前n项和.
(1)若{an}是等差数列,推导Sn的计算公式;
(2)若a1=1,q≠0,且对所有正整数n,有Sn= .判断{an}是否为等比数列,并证明你的结论.
.判断{an}是否为等比数列,并证明你的结论.
解:(1)设{an}的公差为d,
则Sn=a1+a2+…+an
=a1+(a1+d)+…+[a1+(n-1)d],
又Sn=an+(an-d)+…+[an-(n-1)d],
∴2Sn=n(a1+an),
∴Sn= .
.
(2)当n=1时,S1=1.
当n=2时,S2= =1+q,a1+a2=1+q,a2=q.
=1+q,a1+a2=1+q,a2=q.
当n=3时,S3= =1+q+q2,a1+a2+a3=1+q+q2,a3=q2;
=1+q+q2,a1+a2+a3=1+q+q2,a3=q2;
初步断定数列{an}为等比数列.
证明如下:
∵Sn= ,
,
∴an+1=Sn+1-Sn= -
-
= =qn.
=qn.
∵a1=1,q≠0,
∴当n≥1时,有 =
= =q,
=q,
因此,{an}是首项为1且公比为q的等比数列.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
 的前n项和为
的前n项和为 ,且
,且 ,
, .
. 的前n项和为
的前n项和为 ,且
,且  (
( 为常数).令
为常数).令
 .求数列
.求数列 的前n项和
的前n项和 .
. (B)-
(B)- (C)
(C) =
=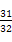 ,则{an}的通项公式an= .
,则{an}的通项公式an= .  +
+ +…+
+…+ 等于( )
等于( ) (B)
(B)
 (D)
(D)
 -10.
-10. 的前
的前 项和
项和 ,则其通项
,则其通项 = ;
= ; 的通项公式
的通项公式 ,求数列
,求数列 。
。