题目内容
平行六面体ABCD-A1B1C1D1中,以顶点A为端点的三条棱长度都为2,且两两夹角为60°,则DB1和C1A1所成角大小为 .
考点:异面直线及其所成的角
专题:空间角
分析:设
=
,
=
,
=
,则两两夹角为60°,且模均为2.|
|=
=2
,|
|=
=2
,
•
=(
-
+
)•(
-
)=4,设DB1和C1A1所成角为θ,cosθ=|cos<
,
>|=
,由此能求出DB1和C1A1所成角大小.
| AB |
| a |
| AD |
| b |
| AA1 |
| c |
| DB1 |
(
|
| 6 |
| C1A1 |
(-
|
| 2 |
| DB1 |
| C1A1 |
| a |
| b |
| c |
| a |
| b |
| DB1 |
| C1A1 |
|
| ||||
|
|
解答:
解:设
=
,
=
,
=
,则两两夹角为60°,且模均为2.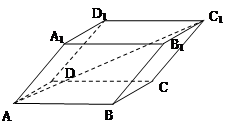
∵
=
-
+
,
=-
-
,
∴|
|=
=
=2
,
|
|=
=
=
=2
,
•
=(
-
+
)•(
-
)
=
2+
2-2
•
+
•
-
•
=4+4-4+2-2
=4,
设DB1和C1A1所成角为θ,
cosθ=|cos<
,
>|=
=
=
,
∴θ=arccos
.
故答案为:arccos
.
| AB |
| a |
| AD |
| b |
| AA1 |
| c |
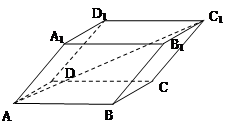
∵
| DB1 |
| a |
| b |
| c |
| C1A1 |
| a |
| b |
∴|
| DB1 |
(
|
=
4+4+4+2×2×2×
|
=2
| 6 |
|
| C1A1 |
(-
|
a2+b2+2
|
=
2+2+2×2×2×
|
| 2 |
| DB1 |
| C1A1 |
| a |
| b |
| c |
| a |
| b |
=
| a |
| b |
| a |
| b |
| a |
| c |
| b |
| c |
=4+4-4+2-2
=4,
设DB1和C1A1所成角为θ,
cosθ=|cos<
| DB1 |
| C1A1 |
|
| ||||
|
|
=
| 4 | ||||
2
|
| ||
| 6 |
∴θ=arccos
| ||
| 6 |
故答案为:arccos
| ||
| 6 |
点评:本题考查的知识点是异面直线所成角的余弦值的计算,考查空间两点之间的距离运算,根据已知条件,构造向量,将空间两点之间的距离转化为向量模的运算,是解答本题的关键.

练习册系列答案
相关题目
已知θ∈(0,π),sinθ+cosθ=
,则tanθ的值为( )
| ||
| 2 |
A、-
| ||||||
B、-
| ||||||
C、-
| ||||||
D、-
|
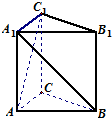 直三棱柱ABC-A1B1C1中,AC=AB=AA1,且异面直线AC1与A1B所成的角为60°,则∠CAB等于
直三棱柱ABC-A1B1C1中,AC=AB=AA1,且异面直线AC1与A1B所成的角为60°,则∠CAB等于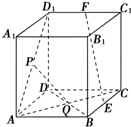 如图,在棱长为a的正方体ABCD-A1B1C1D1中,E、F、P、Q分别是BC、C1D1、AD1、BD的中点.
如图,在棱长为a的正方体ABCD-A1B1C1D1中,E、F、P、Q分别是BC、C1D1、AD1、BD的中点.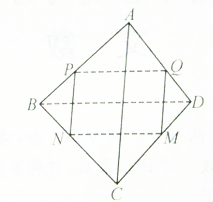 如图,在四面体ABCD中,截面PQMN是平行四边形.
如图,在四面体ABCD中,截面PQMN是平行四边形.