题目内容
5.已知函数f(x)=sin2x+kcos2x的一条对称轴方程为$x=\frac{π}{6}$,则k=$\frac{\sqrt{3}}{3}$.分析 利用辅助角公式基本公式将函数化为y=Asin(ωx+φ)的形式,根据对称轴方程即可求出k的值.
解答 解:函数f(x)=sin2x+kcos2x=$\sqrt{1+{k}^{2}}sin(2x+θ)$,其中tanθ=k.
∵$x=\frac{π}{6}$是其中对称轴,
∴2×$\frac{π}{6}+θ=kπ+\frac{π}{2}$,
∴θ=$kπ+\frac{π}{6}$,k∈Z.
那么:k=tanθ=tan($\frac{π}{6}$)=$\frac{\sqrt{3}}{3}$.
故答案为:$\frac{\sqrt{3}}{3}$.
点评 本题主要考查三角函数的图象和性质,利用三角函数公式将函数进行化简是解决本题的关键.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
16.将函数$y=sin(x-\frac{π}{3})$的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再向右平移$\frac{π}{3}$个单位,所得图象的解析式是( )
| A. | y=sin2x | B. | $y=sin(\frac{x}{2}-\frac{π}{6})$ | C. | $y=-cos\frac{x}{2}$ | D. | $y=sin(2x-\frac{π}{6})$ |
13.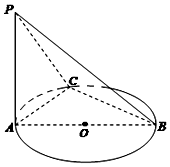 如图,AB是⊙O的直径,PA垂直于⊙O所在平面,C是圆周上不同于A,B两点的任意一点,且AB=2,$PA=BC=\sqrt{3}$,则直线PC与底面ABC所成角的大小为( )
如图,AB是⊙O的直径,PA垂直于⊙O所在平面,C是圆周上不同于A,B两点的任意一点,且AB=2,$PA=BC=\sqrt{3}$,则直线PC与底面ABC所成角的大小为( )
 如图,AB是⊙O的直径,PA垂直于⊙O所在平面,C是圆周上不同于A,B两点的任意一点,且AB=2,$PA=BC=\sqrt{3}$,则直线PC与底面ABC所成角的大小为( )
如图,AB是⊙O的直径,PA垂直于⊙O所在平面,C是圆周上不同于A,B两点的任意一点,且AB=2,$PA=BC=\sqrt{3}$,则直线PC与底面ABC所成角的大小为( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
20.设△ABC的内角A,B,C的对边分别为a,b,c,若a=b,acosC=c(2-cosA),则cosB=( )
| A. | $\frac{{\sqrt{15}}}{4}$ | B. | $\frac{1}{4}$ | C. | $\frac{{\sqrt{3}}}{4}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
2.一个几何体的三视图如图所示,其中俯视图为正方形,则最长侧棱(不包括底面的棱)的长度为( )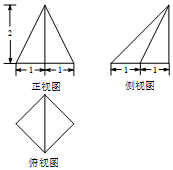

| A. | 2 | B. | $\sqrt{6}$ | C. | $2\sqrt{2}$ | D. | $2\sqrt{3}$ |