题目内容
1．已知$\overrightarrow{a}$=（1，-2），$\overrightarrow{b}$=（-1，3），若m$\overrightarrow{a}$+$\overrightarrow{b}$与$\overrightarrow{a}$-m$\overrightarrow{b}$垂直，求实数m的值．分析 根据向量的数量积和向量的垂直即可求出．
解答 解：∵$\overrightarrow{a}$=（1，-2），$\overrightarrow{b}$=（-1，3），
∴$\overrightarrow{a}$•$\overrightarrow{b}$=1×（-1）-2×3=-7，|$\overrightarrow{a}$|=$\sqrt{5}$，|$\overrightarrow{b}$|=$\sqrt{10}$，
∵m$\overrightarrow{a}$+$\overrightarrow{b}$与$\overrightarrow{a}$-m$\overrightarrow{b}$垂直，
∴（m$\overrightarrow{a}$+$\overrightarrow{b}$）（$\overrightarrow{a}$-m$\overrightarrow{b}$）=m|$\overrightarrow{a}$|2-m|$\overrightarrow{b}$|2+（1-m2）$\overrightarrow{a}$•$\overrightarrow{b}$=5m-10m-7（1-m2）=0，
即7m2-5m-7=0，
解得m=$\frac{5±\sqrt{221}}{14}$
点评 本题考查了向量的数量积的运算和向量的模以及向量的垂直，属于基础题
练习册系列答案
相关题目
4．若f（x）为奇函数，且x0是函数y=f（x）-ex的一个零点，在下列函数中，-x0一定是其零点的函数是（ ）
| A． | y=f（-x）•e-x-1 | B． | y=f（x）•e-x+1 | C． | y=f（x）•e-x-1 | D． | y=f（x）•ex+1 |
2．若不等式n2-n（λ+1）+7≥λ，对一切n∈N*恒成立，则实数λ的取值范围（ ）
| A． | λ≤3 | B． | λ≤4 | C． | 2≤λ≤3 | D． | 3≤λ≤4 |
13．条件p：|x+1|＞2；条件q：{x|2＜x＜3}，则?p是?q的（ ）
| A． | 必要不充分条件 | B． | 充要条件 | ||
| C． | 充分不必要条件 | D． | 既不充分也不必要条件 |
10．棱长为1的正方体截去一部分之后余下的几何体，其三视图如图所示，则余下几何体体积的最小值为（ ）
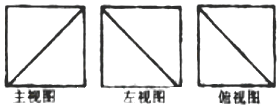
| A． | $\frac{5}{6}$ | B． | $\frac{1}{2}$ | C． | $\frac{2}{3}$ | D． | $\frac{1}{3}$ |