题目内容

18．若角α，β的终边关于x轴对称，则α，β之间的关系是α+β=2kπ（k∈Z）．

分析 根据因为角α和角β的终边关于x轴对称，求出角α 与角β的关系即可．

解答 解：因为角α和角β的终边关于x轴对称，
所以α+β=2kπ（k∈Z）．
故答案为：α+β=2kπ（k∈Z）．

点评 本题主要考查两个角的终边关于x轴对称的性质，属于基础题．

练习册系列答案
相关题目
8．已知双曲线：x2-$\frac{{y}^{2}}{4}$=1上一点P到它的一个焦点的距离为2，则它到另一个焦点的距离为（　　）
A．3B．4C．6D．2+2$\sqrt{5}$
9．已知θ是第三象限角，且sinθ-2cosθ=-$\frac{2}{5}$，则sinθ+cosθ=-$\frac{31}{25}$．
6．下列说法正确的是（　　）
A．函数y=sinx•cosx的最大值为1
B．将y=sin（2x+$\frac{π}{4}$）图象向右平移$\frac{π}{8}$个单位，再将所得图象上各点的横坐标变为原来的2倍，得到正弦函数y=sinx的图象
C．函数f（x）=1-$\frac{1}{x}$在（-∞，0）上是减函数
D．函数f（x）=$\frac{1}{x}$-x的图象关于y轴对称
13．已知$\overrightarrow{a}$=（1，2），$\overrightarrow{b}$=（-3，2），当实数k为何值时，
（Ⅰ）k$\overrightarrow{a}$+$\overrightarrow{b}$与$\overrightarrow{a}$-3$\overrightarrow{b}$垂直？
（Ⅱ）k$\overrightarrow{a}$+$\overrightarrow{b}$与$\overrightarrow{a}$-3$\overrightarrow{b}$平行？平行时它们是同向还是反向？
3．若直线l经过两点A（1，2），B（3，4），则l的倾斜角为$\frac{π}{4}$．
10．已知等差数列{an}满足，若a22+a52=5．则S7的最大值是$\frac{35}{3}$．
7．已知圆C与y轴相切，圆心在直线x-2y=0上，且被x轴的正半轴截得的弦长为2$\sqrt{3}$．
（1）求圆C的方程；
（2）若点P（x，y）在圆C上，x2+y2-4y的取值范围．
8．已知函数y=x（x-2）的定义域为[a，b]，值域为[-1，3]，则点（a，b）对应图中的（　　）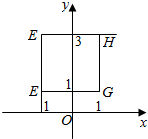
A．点H（1，3）和点F（-1，1）B．线段EF和线段GHC．线段EH和线段FGD．线段EF和线段EH

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网